SOLUTION: Endpoints of minor axis (1, 3) and (1, -1), focus at (-1, 1). Find the equation of the ellipse and sketch the graph.

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Endpoints of minor axis (1, 3) and (1, -1), focus at (-1, 1). Find the equation of the ellipse and sketch the graph.      Log On


   

Question 1170894: Endpoints of minor axis (1, 3) and (1, -1), focus at (-1, 1). Find the equation of the ellipse and sketch the graph.
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
Endpoints of minor axis (1, 3) and (1, -1),
minor axis length is distance between endpoints
so, 2b=4->b=2

center is half way between:
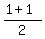+C(h,k)=(%281%2B1%29%2F2,%283-1%29%2F2)=(1,1)
=>
h=1
k=1
focus at (-1, 1) , and c is distance from foci to center which is
c=2
then
a=sqrt%28b%5E2%2Bc%5E2%29
a=sqrt%282%5E2%2B2%5E2%29
a=sqrt%288%29

the equation of the ellipse:
%28x-h%29%5E2%2Fa%5E2%2B%28y-k%29%5E2%2Fb%5E2=1...substitute values for h,k,a,b
%28x-1%29%5E2%2F%28sqrt%288%29%29%5E2%2B%28y-1%29%5E2%2F2%5E2=1
%28x-1%29%5E2%2F8%2B%28y-1%29%5E2%2F4=1