Question 1170892: Consider set A to include all the natural numbers from 1 to 4n, let S be the sum 1+2+3...4n. Now lets randomly partition set A into n subsets each with exactly 4 numbers. Prove that you can pick 2 numbers from each subset so that the sum of resulting 2n numbers will be equal to S/2
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Consider set A to include all the natural numbers from 1 to 4n, let S be the sum 1+2+3...4n.
Now lets randomly partition set A into n subsets each with exactly 4 numbers.
Prove that you can pick 2 numbers from each subset so that the sum of resulting 2n numbers will be equal to S/2.
~~~~~~~~~~~~~~~~~
Solution
It is very interesting problem of the level much higher than the average school level.
It is a Math Olympiad level or a Math circle level problem.
The solution requires several logical steps.
Watch attentively each my step.
(1) The sum 1 + 2 + 3 + 4 + . . . + 4n is equal to S = 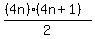 = 2n*(2n+1).
Notice that this sum is an EVEN number -- I will use it in the solution which follows.
(2) Let introduce some designations.
The problem asks about two sums of 2n numbers each.
Let B designates one sequence of 2n numbers, and let = 2n*(2n+1).
Notice that this sum is an EVEN number -- I will use it in the solution which follows.
(2) Let introduce some designations.
The problem asks about two sums of 2n numbers each.
Let B designates one sequence of 2n numbers, and let  be the sum of numbers from B.
Let C designates the other set of 2n numbers, and let be the sum of numbers from B.
Let C designates the other set of 2n numbers, and let 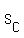 be the sum of numbers from C.
(3) Notice that be the sum of numbers from C.
(3) Notice that  + + 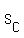 = S = 2n*(2n+1) is an EVEN number.
It implies that the numbers = S = 2n*(2n+1) is an EVEN number.
It implies that the numbers  and and 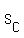 are EITHER both even OR both ODD.
It can not happen that one of are EITHER both even OR both ODD.
It can not happen that one of  and and 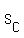 is an even number, while the other is an odd number.
The numbers is an even number, while the other is an odd number.
The numbers  and and 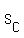 are of the same parity, and their difference is ALWAYS an EVEN number.
(4) The problem requires to prove that it is possible to construct the sets/(the sequences) B and C in a way that are of the same parity, and their difference is ALWAYS an EVEN number.
(4) The problem requires to prove that it is possible to construct the sets/(the sequences) B and C in a way that  = = 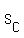 = S/2.
We can start by constructing the sets/(the sequences) B and C of 2n terms each
by an ARBITRARY way in accordance with the imposed conditions.
If eventually it will be = S/2.
We can start by constructing the sets/(the sequences) B and C of 2n terms each
by an ARBITRARY way in accordance with the imposed conditions.
If eventually it will be  = = 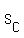 , then everything is Ok and the problem is just solved.
If, on the contrary, , then everything is Ok and the problem is just solved.
If, on the contrary,  =/= =/= 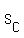 , let say , let say  < < 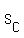 , then I will find two numbers,
b from B and c from C, that differ by 1 unit such that b = c-1, and will permute b to C and c to B.
By doing it, I will increase the sum , then I will find two numbers,
b from B and c from C, that differ by 1 unit such that b = c-1, and will permute b to C and c to B.
By doing it, I will increase the sum  by 1 unit and decrease the sum by 1 unit and decrease the sum 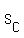 by 1 unit,
diminishing the difference by 1 unit,
diminishing the difference 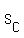 - -  by 2 (two) units.
(5) By repeating this procedure several times (as many times as needed), I will get new sets B and C with by 2 (two) units.
(5) By repeating this procedure several times (as many times as needed), I will get new sets B and C with  = = 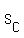 = S/2.
It proves the statement that has to be proved.
+--------------------------------------------------------+
| The method I use is called the "descent" method. |
+--------------------------------------------------------+
(6) The only statement which remained to be proved is THIS
In the sets B and C, such that = S/2.
It proves the statement that has to be proved.
+--------------------------------------------------------+
| The method I use is called the "descent" method. |
+--------------------------------------------------------+
(6) The only statement which remained to be proved is THIS
In the sets B and C, such that  < < 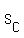 , it is always possible to find
elements b (from B) and c (from C) that differ in one unit, with c = b+1.
But this statement is almost evident/obvious: if you assume the opposite, you quickly will get CONTRADICTION. , it is always possible to find
elements b (from B) and c (from C) that differ in one unit, with c = b+1.
But this statement is almost evident/obvious: if you assume the opposite, you quickly will get CONTRADICTION.
-------------
At this point, I completed my proof.
|
|
|