Question 1170859: find the values of A,B,C if (x-1),(x+2) and (x-2) are factor of
2Ax^4-Bx^3-Cx-16
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52795)   (Show Source):
You can put this solution on YOUR website! .
In accordance with the Remainder theorem, the given part means that the given polynomial has the roots of 1, -2 and 2.
So we write these three equations expressing this fact
2A*1^4 - B*1^3 - C*1 - 16 = 0
2A*(-2)^4 - B*(-2)^3 - C*(-2) - 16 = 0
2A*2^4 - B*2^3 - C*2 - 16 = 0
or
2A - B - C = 16 (1)
32A + 8B + 2C = 16 (2)
32A - 8B - 2C = 16 (3)
Adding equations (2) and (3), you get
64A = 32, which implies A = 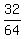 = 0.5.
Then from (1) and (2), substituting A = 0.5 there, you get
B + C = -15 (4)
8B + 2C = 0 (5)
Expressing B = -15 - C from (4) and substituting it to (5), you get
8*(-15 -C) + 2C = 0, or
-120 - 8C + 2C = 0
- 6C = 120
C = - 20.
Then from equation (4), B = -15 - (-20) = -15 + 20 = 5.
ANSWER. A = 0.5; B = 5, C = -20.
Solved.
Answer by math_tutor2020(3817)  (Show Source):
You can put this solution on YOUR website!
We have three factors: (x-1),(x+2) and (x-2)
However, we have a quartic polynomial, since the degree (largest exponent) is 4
So we need a fourth factor. Let's call that x-p, for some real number p.
Let's expand out the following
(x-1)(x+2)(x-2)(x-p)
(x+2)(x-2)(x-1)(x-p)
(x^2-4)(x^2-px-x+p)
x^2(x^2-px-x+p)-4(x^2-px-x+p)
x^4-px^3-x^3+px^2-4x^2+4px+4x-4p
x^4+(-px^3-x^3)+(px^2-4x^2)+(4px+4x)-4p
x^4+(-p-1)x^3+(p-4)x^2+(4p+4)x-4p
Compare that result to 2Ax^4-Bx^3-Cx-16
Match up the corresponding terms, and we have the following equations
- 2Ax^4 = 1x^4 which leads to 2A = 1 and solves to A = 1/2 = 0.5
- (-p-1)x^3 = -Bx^3 which leads -p-1 = -B and solves to B = p+1
- (4p+4)x = -Cx which leads to 4p+4 = -C and solves to C = -4p-4
- -4p = -16 which solves to p = 4
Use that value of p to find the other coefficients
B = p+1 = 4+1 = 5
C = -4p-4 = -4*4-4 = -20
The polynomial 2Ax^4-Bx^3-Cx-16 turns into x^4-5x^3+24x-16 after we plug in those A,B, and C values.
Answers:
A = 1/2 = 0.5
B = 5
C = -20
|
|
|
