SOLUTION: A certain disease has an incidence rate of 0.6%. If the false negative rate is 4% and the false positive rate is 1%, compute the probability that a person who tests positive actual

This problem is on conditional probability, and I will put things in order.


Originally, we have a whole population of X people.

0.6% of them, or 0.006*X, have the disease.

The rest, or 0.994*X, do not have the disease (are healthy).


The number of those who actually has the disease AND has test positive is  n = (1-0.04)*(0.006*X) = 0.96*0.006*X.


The number of those who are test positive is the sum  N = 0.96*(0.006*x) + 0.01*(0.994*X).


In this sum, first  addend comes from the set of people having the disease; 
             second addend comes from the set of people who do not have the disease.


The problem wants you find the conditional probability, which is the ratio n/N.  It is 

    P =  = .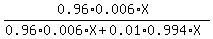


Now reduce X in the numerator and in the denominator.  You will get

    P =  =  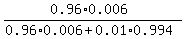=  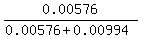=  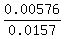= 0.3669  (rounded), or 36.69%.



       So, the effectiveness of such a test is, actually, lower than expected.


The major reason, WHY it is so low, is that the contribution of false positive tests is very big.

When the incidence rate is low, it leads to loss of effectiveness of testing.



When the incidence rate is low, the requirements to the test to be effective are very low false positive rates.