Question 1170690: A certain disease has an incidence rate of 0.2%. If the false negative rate is 5% and the false positive rate is 5%, compute the probability that a person who tests positive actually has the disease.
Answer by ikleyn(52815)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A certain disease has an incidence rate of 0.2%. If the false negative rate is 5% and the false positive rate is 5%,
compute the probability that a person who tests positive actually has the disease.
~~~~~~~~~~~~~~~~~~~~~~~~~~
This problem is on conditional probability, and I will put things in order.
Originally, we have a whole population of X people.
0.2% of them, or 0.002*X, have the disease.
The rest, or 0.998*X, do not have the disease (are healthy).
The number of those who actually has the disease AND has test positive is n = (1-0.05)*(0.002*X) = 0.95*0.002*X.
The number of those who are test positive is the sum N = 0.95*(0.002*x) + 0.05*(0.998*X).
In this sum, first addend comes from the set of people having the disease;
second addend comes from the set of people who do not have the disease.
The problem wants you find the conditional probability, which is the ratio n/N. It is
P =  = = 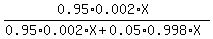 .
Now reduce X in the numerator and in the denominator. You will get
P = .
Now reduce X in the numerator and in the denominator. You will get
P =  = = 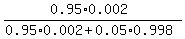 = = 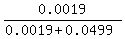 = = 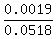 = 0.03668 (rounded), or 3.668%. = 0.03668 (rounded), or 3.668%.
Solved.
|
|
|