Question 1170631: Solve by using substitution method or elimination method:
A bakery bakes three types of bread with the monthly cost being RM6850 for 2150 loaves of bread. The cost of baking a load of butterscotch bread is RM2, a chocolate bread is RM3 and a coconut bread RM4. The sale prices of a loaf of butterscotch bread, a chocolate bread and a coconut bread are RM3, RM4.50 and RM5.50 respectively. If the bakery makes a profit of RM2975 monthly, how many loaves of each type of bread will it bake?
Found 2 solutions by Theo, MathTherapy:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! let a = number of butterscotch breads
let b = number of chocolate breads
let c = number of coconut breads.
your solution is:
a = 500
b = 750
c = 900
your original equations are:
2a + 3b + 4c = 6850
a + b + c = 2150
a + 1.5b + 1.5c = 2975
replace the variables with their respective values to get:
2*500+ 3*750 + 4*900 = 6850
500 + 750 + 900 = 2150
500 + 1.5*750 + 1.5*900 = 2975
this confirms the solution is correct.
i used a gaussian elimination calculator such as the one found at https://onlinemschool.com/math/assistance/equation/gaus/
if you were to do this manually, you would probably do the following, or something that, the goal being to get your matrix into a form of:
xa 0 0 t1
0 yb 0 t2
0 0 zc t3
you could stop there, or you could go a step further and get your matrix into a form of:
1a 0 0 t1
0 1b 0 t2
0 0 1c t3
both forms will get you the answer.
in the first form, however, you will need to go one extra step, such as:
a = t1/x
b = t2/y
c = t3/z
while, in the second form, that has already been done and you can just read off the answer as:
a = t1
b = t2
c = t3
the t's in the first form would, naturally, not be the same values as the t's in the second form, since the division was already done in the second form.
the a,b,c in the first form, however, would be the same as the a,b,c in the second form, once the final divisions were performed.
i took a stab at doing this manually, just to see if i could get the same answer.
i was successful.
my effort is shown below.
it's a little sloppy, but you should be able to get the idea from it as to how the procedure works.
the are different procedures that will work.
the one below is just one tactic that was used.
the goal is to get the matrix into one of the forms i shows you above.
i just happened to get to the second form, which was actually quite good for a first effort.
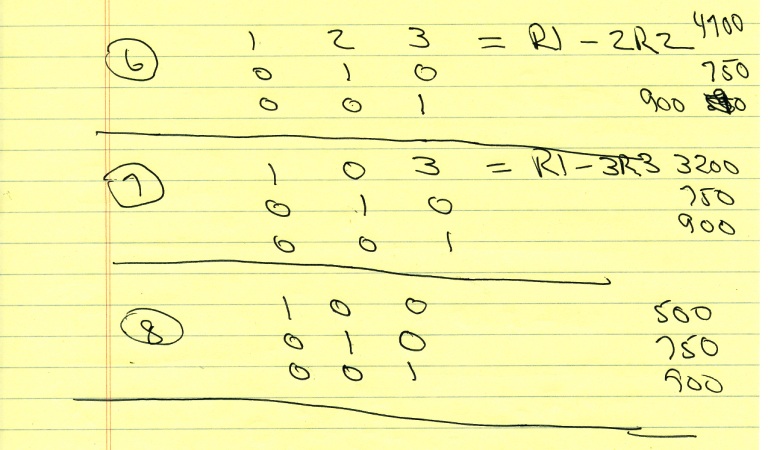
in step 1, i just copied down the matrix.
that's the 3 equations with only the coefficients and the constants showing.
in step 2, i replaced row 3 with the calculation of row 1 minus 2 * row 3 from step 1.
that's what R1 - 2R3 means on row 3 of the matrix in step 1.
in step 3, i replaced row 1 with the calculation of row 1 minus row 2 from step 2.
that's what R1 - R2 means on row 1 of the matrix in step 2.
in step 4, i screwed it up and just crossed it out and repeated step 4 below that.
i replaced row 2 with the calculation of row 2 minus row 1 from step 3.
in step 5, i replaced row 2 with the calculation of row 2 + 2 * row 3 from step 4.
in step 6, i replaced row 2 with the calculation of row 2 * -1 from step 5.
in step 7, i replaced row 1 with the calculation of row 1 - 2 * row 2 from step 6.
in step 8, i replaced row 1 with the calculation of row 1 - 3 * row 2 from step 7.
you are free to use the mechanized calculator to see if you get the same results.
in doing that, you can also see the steps that the calculator used to get to the final answer.
they are not necessarily the steps that i took manually.
there are various ways to get the same answer.
some are more efficient than others.
Answer by MathTherapy(10552)  (Show Source):
You can put this solution on YOUR website! Solve by using substitution method or elimination method:
A bakery bakes three types of bread with the monthly cost being RM6850 for 2150 loaves of bread. The cost of baking a load of butterscotch bread is RM2, a chocolate bread is RM3 and a coconut bread RM4. The sale prices of a loaf of butterscotch bread, a chocolate bread and a coconut bread are RM3, RM4.50 and RM5.50 respectively. If the bakery makes a profit of RM2975 monthly, how many loaves of each type of bread will it bake?
I don't see anywhere here where you asked for the problem to be solved using MATRICES, so I wonder why the other person would use that method.
Plus, not everyone knows or may care to use matrices when solving equations. Then again, the person who responded is none other that Mr. EXTRAVAGANT and COMPLEX!
You also don’t need any fancy equipment or software to solve this problem!
Let number of butterscotch, chocolate, and coconut baked and sold, be B, C, and D, respectively
Then the number-of-loaves equation is: B + C + D = 2,150 ------ eq (i)
Also, the cost-equation is: 2B + 3C + 4D = 6,850 ------ eq (ii)
And, the PROFIT equation is: 3B + 4.5C + 5.5D - (2B + 3C + 4D) = 2,975
3B + 4.5C + 5.5D - 2B - 3C - 4D = 2,975
B + 1.5C + 1.5D = 2,975 ------- eq (iii)
2B + 3C + 3D = 5,950 ------- Multiplying eq (iii) by 2 ------- eq (iv)
D = 900 ------ Subtracting eq (iv) from eq (ii)
Number of coconut bread it'll bake, or 
B + C + 900 = 2,150 ------ Substituting 900 for D in eq (i)
B + C = 1.250 ------ eq (v)
2B + 3C + 4(900) = 6,850 ------ Substituting 900 for D in eq (ii)
2B + 3C = 3.250 ------ eq (vi)
2B + 2C = 2,500 ------ Multiplying eq (v) by 2 ------ eq (vii)
Number of chocolate loaves to be baked, or  ------- Subtracting eq (vii) from eq (vi)
B + 750 + 900 = 2,150 ------ Substituting 900 for D, and 750 for C in eq (i)
B + 1,650 = 2.150
Number of butterscotch loaves to be baked, or 
|
|
|
