Instead of doing your problem for you, I'll do one exactly like yours, with
different numbers and in feet, not meters. Use it as a model to do yours by.
A tunnel through a mountain for a four lane highway is to have an elliptical
opening. The total width of the highway(not the opening) is to be 48 ft and the
height at the edge of the road must be sufficient for a truck 11 ft high to
clear if the highest point of the opening is to be 15 ft approximately. How
wide must the opening be?
 The semi-ellipse must be as above. We put the center at the origin. Since the
height is 15 feet, the semi-minor axis = b = 15.
The total width of the highway is 48 feet, so each lane must be 24 feet wide.
For a truck 11 feet high to just scrape the top of the tunnel, when its
right side is at the edge of the highway, the ellipse must pass through the
point (24,11), and also the point (-24,11).
[Note: It would be more practical to make to make it 1 foot higher, to go
through (24,12) instead of (24,11) so that an 11-foot tall truck would have a
1-foot clearance and not scrape the top, but the problem didn't state any
clearance, so I will let the truck scrape the top at the edge of the highway]
The equation of an ellipse is
The semi-ellipse must be as above. We put the center at the origin. Since the
height is 15 feet, the semi-minor axis = b = 15.
The total width of the highway is 48 feet, so each lane must be 24 feet wide.
For a truck 11 feet high to just scrape the top of the tunnel, when its
right side is at the edge of the highway, the ellipse must pass through the
point (24,11), and also the point (-24,11).
[Note: It would be more practical to make to make it 1 foot higher, to go
through (24,12) instead of (24,11) so that an 11-foot tall truck would have a
1-foot clearance and not scrape the top, but the problem didn't state any
clearance, so I will let the truck scrape the top at the edge of the highway]
The equation of an ellipse is
 +
+  = 1
But since the center is (h,k) = (0,0), the equation simplifies to
= 1
But since the center is (h,k) = (0,0), the equation simplifies to
 +
+  = 1
We know that b = 15, so we have
= 1
We know that b = 15, so we have
 +
+  = 1
= 1
 +
+  = 1
Since it goes through the point (24,11), we substitute (x,y) = (24,11)
= 1
Since it goes through the point (24,11), we substitute (x,y) = (24,11)
 +
+ 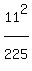 = 1
= 1
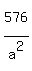 +
+ 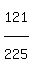 = 1
Solve that for "a" and get
a = 35.30090432, the semi-major axis.
The width of the opening must be the entire major axis,
so the answer to this problem is twice that or 70.60180865 feet.
Now do yours the exact same way step by step.
Edwin
= 1
Solve that for "a" and get
a = 35.30090432, the semi-major axis.
The width of the opening must be the entire major axis,
so the answer to this problem is twice that or 70.60180865 feet.
Now do yours the exact same way step by step.
Edwin