Question 117046: Find the number of distinguishable permutations of the group of letters: A,A,G,E,E,E,M.
Found 2 solutions by edjones, MathLover1:
Answer by edjones(8007)   (Show Source): (Show Source):
You can put this solution on YOUR website! 7!/2!*3! In the denominator the letters that appear more than once are factorialized.
=7*6*5*4*3*2/3*2*2
=7*5*4*3 the 6 is canceled by 3*2 and 2 is canceled by 2.
=420
Ed
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find the number of distinguishable permutations of the group of letters:  , , , ,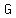 , , , , , , , , . .
Here are the frequencies of the letters:  , ,  , ,  , ,  for a total of for a total of  letters. letters.

Then the number of distinguishable permutations will be:
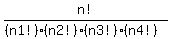
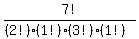
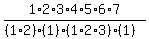
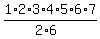 ……… do some simplification ……… do some simplification

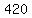
so, the number of distinguishable permutations of the group of letters is  . .
|
|
|