Question 1170262: find the three cube roots of 6-2i and express the roots in polar form.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! find the three cube roots of 6-2i and express the roots in polar form.
First we plot the point 6-2i which is the point (6,-2), x=6, y=-2
We draw a vector from(0,0) to (6,-2).

The hypotenuse is  , but we'll leave it , but we'll leave it 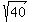 for now. for now.
Calculate θ by  , so , so 
So 6-2i in polar form is

We can add any integer times 360° to the angle without changing the value:


We raise both side to the 1/3 power, the same as taking cube root, and write
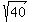 as the 1/2 power of 40 as the 1/2 power of 40

Next we use DeMoivre's theorem, which is to raise the modulus to the 1/3
power and multiply the argument by 1/3:


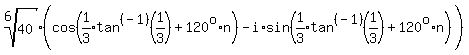 where n=0,1,2 where n=0,1,2
[Write all three values out].
Or if you want it in radians, substitute  for 120° for 120°
Edwin
|
|
|