 First we replace the green g(x) by the right side of g(x), which is x3:
First we replace the green g(x) by the right side of g(x), which is x3:
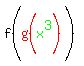 Next we must find
Next we must find 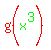 , which means to substitute
x3 for x in the right side of g(x), which is also x3, so we get
, which means to substitute
x3 for x in the right side of g(x), which is also x3, so we get 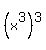 which is
which is 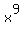 So
So  So we substitute x9 for
So we substitute x9 for 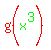 in
in
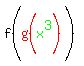 and get
and get
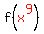 That means to substitute x9 for x in the right side of f(x), which
is tan(x) + 1, so the final answer is:
That means to substitute x9 for x in the right side of f(x), which
is tan(x) + 1, so the final answer is:
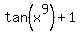 Edwin
Edwin