Question 1170096: "Find the zeros of the polynomial equation X^4 + 2X^3 - 13X^2 - 14X + 24 = 0"
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
As a teaching tool, the response from the other tutor is, as far as I can see, of no use, since there is no explanation of her initial step for writing each term as the sum of two like terms.
She might actually know a method for doing that; I am not familiar with any such method.
The easiest way to do this, of course, is with a graphing calculator. But that doesn't teach you anything, so we won't do it that way.
To start with, note that relatively simple algebraic methods can be used to find roots only if the roots are all rational. Assuming that is the case, the usual approach is to use the rational roots theorem and the remainder theorem to find roots and then reduce the polynomial using either long division or synthetic division.
The rational roots theorem tells us the only possible rational roots are positive or negative factors of p/q, where p is the constant term and q is the leading coefficient. In this example, p/q = 24/1 = 24; the possible rational roots are (plus or minus) {1, 2, 3, 4, 6, 8, 12, 24}.
The remainder theorem says that if f(a)=0 then a is a root of the polynomial -- i.e., (x-a) is a factor.
It is easy to check for roots of 1 or -1 by evaluating the polynomial for each of those values. Doing that quickly shows that a=1 is a root. "Factor out" that root using synthetic division:
1 | 1 2 -13 -14 24
| 1 3 -10 -24
+-----------------
1 3 -10 -24 0
So the original polynomial is
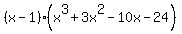
Look for another root using the rational roots theorem and synthetic division.
Without going into details, it turns out x=3 is another root:
3 | 1 3 -10 -24
| 3 18 24
+--------------
1 6 8 0
Now the original polynomial is
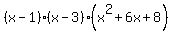
Once the remaining polynomial is reduced to a quadratic, we can find the factorization algebraically:
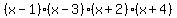
ANSWER: The zeros are 1, 3, -2, and -4
A graph confirms those answers....

|
|
|