Question 1170043: The pilot quickly starts to climb so as to fly the plane over the mountain peak. When he is 2000m away from the mountain peak (2450m in height) in the horizontal direction, and at an altitude of 1850m, he is flying at an angle of 17 (degrees) to the horizontal.
key info:
- the mountain is 2450m tall/ in height
A) if the pilot continues to fly at this angle, will he clear the mountain peak?
B) what is the smallest angle of inclination, to the nearest degree, that the pilot can fly and still clear the mountain peak?
if possible, could you also please provide the working out to both questions and specify which type of formula was expected and which subject of trig was used? thank you so much!
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! The pilot quickly starts to climb so as to fly the plane over the mountain peak. When he is 2000m away from the mountain peak (2450m in height) in the horizontal direction, and at an altitude of 1850m, he is flying at an angle of 17 (degrees) to the horizontal.
key info:
- the mountain is 2450m tall/ in height
Draw a diagram of this scenario, the plane is at an altitude of 1850 and the peak is 2450. 2450-1850 = 600+ more feet he has to climb to clear the mountain. Assuming the the 2000 ft is to a point directly below the peak of the mountain
:
A) if the pilot continues to fly at this angle, will he clear the mountain peak?
A right triangle so we can use the tangent of 17 degrees
h = the addition elevation he will have in 2000ft at a 17 degree angle
tan(17) = 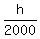
calculate
h = 611.46 ft so he just clears it.
:
B) what is the smallest angle of inclination, to the nearest degree, that the pilot can fly and still clear the mountain peak?
let a = the angle in question
To clear by 1 meter
tan(a) = 601/2000
calculate
a = 16.7 degrees to clear it by 1 meter
|
|
|