Question 116997: This is one question amounst a few more that I have to answer within a essay regarding the Law of Large numbers, is there any way you can help me explain this one please.
Explain your answer to the following question: Is it true that if I get tails 3 times in a row that my chances of getting heads on my next toss is greater than 50%?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Flipping coins
If you want to know the 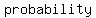 of a coin landing of a coin landing 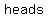 , heads is the favorable outcome. There is , heads is the favorable outcome. There is 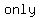 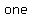 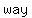 for a coin to land heads, so the for a coin to land heads, so the 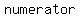 of the of the 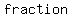 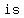  . .
The sample space consists of the total number of ways that a coin can land. Since a coin can  land land  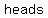 or or 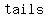 – – 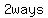 - the sample space is made up of - the sample space is made up of 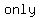  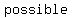 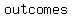 and the denominator of the probability fraction is and the denominator of the probability fraction is  . .
Thus the probability of a coin landing heads is  , which is the same as saying that a coin lands heads , which is the same as saying that a coin lands heads  % of the time. % of the time.
What is the probability of the coin landing tails? We can do the same analysis as for the coin landing heads, finding a probability of  , or, knowing that if a coin doesn't land heads it has to land tails, and understanding that , or, knowing that if a coin doesn't land heads it has to land tails, and understanding that   of the of the 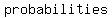 MUST be equal to MUST be equal to  , subtract: , subtract:
the probability of a coin landing tails must be  . .
In this case, 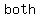 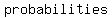 (a 1/2 chance of landing either heads or tails) remain (a 1/2 chance of landing either heads or tails) remain 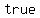 ; NO MATTER HOW MANY TIMES you flip a coin, ; NO MATTER HOW MANY TIMES you flip a coin,  time the coin is EQUALLY likely to fall time the coin is EQUALLY likely to fall 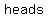 or or 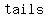 . .
Even if your coin has fallen heads  times times 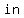  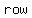 , the chance that the next toss will fall tails is still , the chance that the next toss will fall tails is still  %. %.
So, if you get tails  times in a row your chances of getting heads on your next toss is NOT greater than times in a row your chances of getting heads on your next toss is NOT greater than  %. %.
|
|
|