|
Question 1169939: Good day. May you please assist me in the following question:
Consider the integers x and y. When y is divided by x the remainder is 29. When y is divided by x/2, the remainder is 13. Determine x.
Thank you fro your assistance.
Found 3 solutions by greenestamps, math_helper, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let's look at some examples of what is being done here. Divide one number y by some even integer x and look at the quotient and remainder; and then divide y by x/2 and look at the quotient and remainder.
(1)
13/4 = 3 remainder 1
13/2 = 6 remainder 1
19/6 = 3 remainder 1
19/3 = 6 remainder 1
50/12 = 4 remainder 2
50/6 = 8 remainder 2
In all of these examples, the remainder when divided by the larger divisor is less than half the divisor. The result is that the quotient doubles and the remainder stays the same.
(2)
29/6 = 4 remainder 5
29/3 = 9 remainder 2
29/8 = 3 remainder 5
29/4 = 7 remainder 1
37/10 = 3 remainder 7
37/5 = 7 remainder 2
In these examples, the remainder when divided by the larger divisor is greater than half the divisor. The result is that the quotient is 1 more than doubled, and the remainder is reduced by the smaller divisor.
Those are the only two possible results.
In the given example, the remainder decreases by 16 when divided by the smaller number, x/2.
So x/2 = 16, and x = 2*16 = 32.
ANSWER: x = 32
CHECK (examples)
61/32 = 1 remainder 29
61/16 = 3 remainder 13
157/32 = 4 remainder 29
157/16 = 9 remainder 13
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website! By trial-and-error, x=32.
One way to come to this answer is to set y to 29. Then for any x > 29 and x < 58, it is trivial that 29 mod x = 29. So all that is needed is to check 29 mod (x/2) to find the value of x/2 that has remainder 13. For x=32, we get 29 mod 16 = 13, so the answer x=32 works.
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Consider  positive integer numbers x and y. positive integer numbers x and y.
When y is divided by x the remainder is 29. When y is divided by x/2, the remainder is 13. Determine x.
~~~~~~~~~~~~~~~
You just saw the solutions by other tutors suggesting to use trial and error method.
Meanwhile, the problem admits simple straightforward pure mathematical solution based on reasoning, ONLY.
In my opinion, it is the most suitable solution for this problem.
And I am 179% sure that this solution is what you are seeking for.
(1) Consider the statement "When y is divided by x the remainder is 29".
It means that there is an integer number "n" such that
y = nx + 29, 29 < x. (1)
(2) Consider next statement "When y is divided by x/2, the remainder is 13".
It means that there is an integer number "m" such that
y = 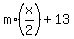 , 13 < , 13 <  . (2)
(3) From equations (1) and (2) we have
nx + 29 = . (2)
(3) From equations (1) and (2) we have
nx + 29 = 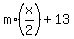 , x > 29
or, equivalently
2nx + 58 = mx + 26, x > 29
58 - 26 = mx - 2nx, x > 29
32 = (m - 2n)x, x > 29 (3)
(4) Thus, the integer number x is a divisor of the number 32, and x > 29.
But the only such integer is x = 32. , x > 29
or, equivalently
2nx + 58 = mx + 26, x > 29
58 - 26 = mx - 2nx, x > 29
32 = (m - 2n)x, x > 29 (3)
(4) Thus, the integer number x is a divisor of the number 32, and x > 29.
But the only such integer is x = 32.
The problem is just solved, and the ANSWER is: the number " x " is 32.
|
|
|
| |