Question 1169901: If the perimeter of a rectangle is 44 cm and the area is 105 square cm, then what are the dimensions of the rectangle?
Answer by ikleyn(52787)   (Show Source):
You can put this solution on YOUR website! .
In my post, I will show you the way to solve the problem MENTALLY, without using equations.
The sum of the length and the width is half of the perimeter, i.e. 22 cm.
Half of the sum is 11 cm. It is the "mean" of the length and the width.
Let "W" be the width; let "L" be the length, and let d = 11 - W be the deviation of the width from the mean.
We have then L = 11 + d; W = 11 - d;
hence, the area 105 = L*W = (11+d)*(11-d) = 121 - d^2,
d^2 = 121 - 105 = 16; d = 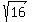 = 4 cm.
Thus the length is L = 11+4 = 15 cm; the width is W = 11-4 = 7 cm. ANSWER
The problem solved MENTALLY, without using equations.
Feel joy having elegant and unexpected solution (!)
---------------
To see many other similar problems, solved in this way, look into the lessons
- Problems on the area and the dimensions of a rectangle
- Three methods to find the dimensions of a rectangle when its perimeter and the area are given
- Three methods to find the dimensions of a rectangle when its area and the difference of two dimensions are given
in this site.
----------------
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic
"Dimensions and the area of rectangles and circles and their elements".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|
