|
Question 1169861: A number of two digits exceeds twice the sum of its digits by 26. If the
digits are interchanged, the resulting number exceeds the given number
by 18. Find the number.
Answer by greenestamps(13216)   (Show Source):
You can put this solution on YOUR website!
A solution using formal algebra....
x = tens digit
y = units digit
10x+y = original number
10y+x = original number with digits reversed
(1) 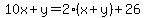 [the number exceeds twice the sum of its digits by 26]
(2) 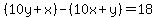 [the number with the digits reversed exceeds the given number by 18]
Use (2) to find y in terms of x:
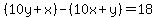
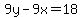
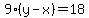
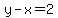
Substitute "x+2" for "y" in (1):
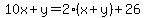
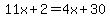
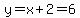
ANSWER: the number is 10x+y = 46
The first calculation above shows that, when a 2-digit number is subtracted from the same number with the digits reversed, the result is always a multiple of 9. If a formal algebraic solution is not required (for example, in a timed math contest where a quick solution is wanted), you can use this fact along with trial and error to quickly find the answer.
Since the difference in this case is 18, we know the difference between the digits is 2; and since the number with the digits reversed is greater than the given number, we know the units digit is 2 more than the tens digit.
So the possible 2-digit numbers are 13, 24, 35, 46, 57, 68, and 79.
Then simply find which of those satisfies the condition that the number exceeds twice the sum of its digits by 26.
|
|
|
| |
