Question 1169792: Hope this is the right topic
Question: Write y(t)=2sin(4πt) + 5cos(4πt) in the form y(t)=A sin(wt+ Φ) and identify the amplitude, angular frequency, and the phase shift of the spring motion.
More background info:
y(t) = distance of weight from equilibrium position
w= angular frequency (measured in radians per second)
A = amplitude
Φ = phase (depends on initial conditions)
c1 = AsinΦ
c2 = AcosΦ
THANK YOU SO MUCH IN ADVANCE FOR HELPING ME!
Found 2 solutions by htmentor, ikleyn:
Answer by htmentor(1343)   (Show Source): (Show Source):
Answer by ikleyn(52908)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
You are given the equation y(t)=2sin4πt+5cos4πt, which models the position of the weight, with respect to time.
You need to find the amplitude of the oscillation, the angular frequency, and the initial conditions of the motion.
You will also be required to find the time(s) at which the weight is at a particular position.
To find this information, you need to convert the equation to the first form, y(t)=Asin(wt+Φ).
Question: Use the information above and the trigonometric identities to prove that Asin(wt+Φ)=c2sinwt+c1coswt .
~~~~~~~~~~~
There is an absolutely standard method solving such problems.
The mathematicians, physicists and electrical engineers know it very well - they do it automatically.
See below and watch attentively each my step.
(1) You re-write the original equation step by step in this form
y(t) = 2*sin(4πt) + 5*cos(4πt) =  . (1)
(2) Consider the coefficients . (1)
(2) Consider the coefficients 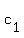 = = 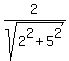 and and  = = 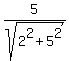 .
Notice that the coefficients .
Notice that the coefficients 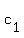 and and  are positive and are positive and 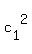 + + 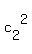 = 1.
Therefore, there is an angle Φ in the first quadrant QI such that cos(Φ) = = 1.
Therefore, there is an angle Φ in the first quadrant QI such that cos(Φ) = 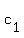 , sin(Φ) = , sin(Φ) =  .
Simply Φ = .
Simply Φ =  .
(3) Therefore, we can re-write (1) in the form
y(t) = .
(3) Therefore, we can re-write (1) in the form
y(t) = 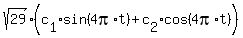 = = 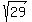 *(cos(Φ)*sin(4πt) + sin(Φ)*cos(4πt)) (2)
(4) Next, apply the formula for sine of the sum of arguments. You can continue writing the formula (2) in this way
y(t) = *(cos(Φ)*sin(4πt) + sin(Φ)*cos(4πt)) (2)
(4) Next, apply the formula for sine of the sum of arguments. You can continue writing the formula (2) in this way
y(t) = 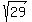 *sin(4πt + Φ).
(5) Now compare it with your formula y(t) = Asin(wt+Φ).
You see that the amplitude A = *sin(4πt + Φ).
(5) Now compare it with your formula y(t) = Asin(wt+Φ).
You see that the amplitude A = 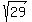 , w = 4π and the phase shift Φ = , w = 4π and the phase shift Φ = 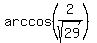 . .
The solution is completed.
To get the numerical values, use your calculator.
|
|
|