Question 1169789: Given a right pyramid ABCDE, on a square base ABCD, with AB = 8 cm, and height EO = 5 cm, what are the values of the following:
(a) angle EAB
(b) angle β between a slant edge and the plane on the base.
(c) angle θ between a slant face and the plane on the base.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1987)   (Show Source):
You can put this solution on YOUR website! Absolutely, let's break down this pyramid geometry problem.
**Understanding the Problem**
We have a right pyramid with a square base. We need to find specific angles related to the pyramid's edges and faces.
**Given Information**
* Base ABCD is a square with side length AB = 8 cm.
* Height of the pyramid EO = 5 cm (where O is the center of the square base).
**Diagram**
It's helpful to visualize the pyramid.
1. Draw a square ABCD.
2. Mark the center of the square as point O.
3. Draw a line segment EO perpendicular to the square base, with EO = 5 cm.
4. Connect point E to each vertex of the square (A, B, C, D) to form the pyramid.
**Solutions**
**(a) Angle EAB**
1. **Triangle EOA:** Triangle EOA is a right triangle, with ∠EOA = 90°.
2. **OA:** Since O is the center of the square, OA is half the length of the diagonal AC.
* AC = √(AB² + BC²) = √(8² + 8²) = √(128) = 8√2 cm.
* OA = (8√2) / 2 = 4√2 cm.
3. **Tangent:** We can use the tangent function to find angle EAB (let's call it α).
* tan(α) = EO / OA = 5 / (4√2)
* α = arctan(5 / (4√2)) ≈ arctan(5 / 5.6568) ≈ arctan(0.884)
* α ≈ 41.52°
Therefore, angle EAB ≈ 41.52°.
**(b) Angle β between a slant edge and the plane on the base.**
1. **Slant Edge EB:** We need to find the angle between the slant edge EB and the base.
2. **Triangle EOB:** Triangle EOB is a right triangle, with ∠EOB = 90°.
3. **OB:** OB is half the length of the diagonal BD, which is equal to AC.
* OB = OA = 4√2 cm.
4. **Tangent:** We can use the tangent function to find angle EBO (β).
* tan(β) = EO / OB = 5 / (4√2)
* β = arctan(5 / (4√2)) ≈ 41.52°
Therefore, angle β ≈ 41.52°.
**(c) Angle θ between a slant face and the plane on the base.**
1. **Slant Face EBC:** We need to find the angle between the slant face EBC and the base ABCD.
2. **Midpoint of BC:** Let M be the midpoint of BC.
3. **Triangle EOM:** Triangle EOM is a right triangle, with ∠EOM = 90°.
4. **OM:** OM is half the length of AB (or CD), so OM = 8 / 2 = 4 cm.
5. **Tangent:** We can use the tangent function to find angle EMO (θ).
* tan(θ) = EO / OM = 5 / 4 = 1.25
* θ = arctan(1.25) ≈ 51.34°
Therefore, angle θ ≈ 51.34°.
**Final Answers**
* **(a) Angle EAB ≈ 41.52°**
* **(b) Angle β ≈ 41.52°**
* **(c) Angle θ ≈ 51.34°**
Answer by ikleyn(52896)  (Show Source):
You can put this solution on YOUR website! .
Given a right pyramid ABCDE, on a square base ABCD, with AB = 8 cm, and height EO = 5 cm,
what are the values of the following:
(a) angle EAB
(b) angle β between a slant edge and the plane on the base.
(c) angle θ between a slant face and the plane on the base.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In the post by @CPhill, his answer to question (a) is INCORRECT;
his answer to question (b) is INNACCURATE.
I came to bring correct solutions and correct answers to posed questions.
Let F be the midpoint of the edge AB at the base of the pyramid.
(a) Then triangle EOF is a right-angled triangle (recall that point O is the foot
of the altitude EO, and is, at the same time, the center of the square ABCD).
Triangle EOF has the legs EO = 8/2 = 4 cm and OF = 5 cm.
Hence, the length of the hypotenuse EF is
EF = 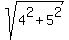 =  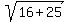=  cm.
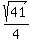Then tangent of angle EAB is  =  =  .
Hence, angle EAB is 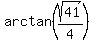 = arctan() = 58.007183 degrees, approximately.
Thus, angle EAB is about 58 degrees.
(b) Angle  between a slant edge and the plane of the base is the angle EAO of triangle EAO.
This triangle is a right-angled triangle.
Its leg EO is 5 cm long; its leg OA is 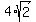 cm long.
Therefor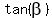e,  =  .
Hence, =  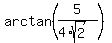= arctan(0.883883476) = 41.4729343 degrees.
Thus, angle is about 41.47 degrees.
(c) angle  between a slant face and the plane on the base is the angle EFO of triangle EFO.
Triangle EFO is a right-angled triangle.
Its leg EO is 5 cm long. Its leg OF is 4 cm long.
Therefore,  =  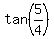= tan(1.25)}}}.
Hence, =  = arctan(1.25) = 51.3401917 degrees.
Thus, angle is about 51.34 degrees.
ANSWER. Angle EAB is about 58 degrees.
Angle is about 41.47 degrees.
Angle is about 51.34 degrees.
Solved correctly.
|
|
|
