Question 1169702: Eugene began to save for his retirement at age 29, and for 11 years he put $ 500 per month into an ordinary annuity at an annual interest rate of 9% compounded monthly. After the 11 years, Eugene was unable to make the monthly contribution of $ 500, so he moved the money from the annuity into another account that earned 12% interest compounded monthly. He left the money in this account for 25 years until he was ready to retire. How much money did he have for retirement?
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Eugene began to save for his retirement at age 29, and for 11 years he put $ 500 per month
into an ordinary annuity at an annual interest rate of 9% compounded monthly.
After the 11 years, Eugene was unable to make the monthly contribution of $ 500,
so he moved the money from the annuity into another account that earned 12% interest compounded monthly.
He left the money in this account for 25 years until he was ready to retire.
How much money did he have for retirement?
~~~~~~~~~~~~~~~~~~~~~~
Solve it in two steps.
First, determine future value FV1 of the account after first 11 years.
Use the standard formula for the ordinary annuity
FV1 = 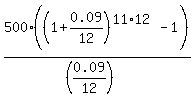 = 112,087.42 dollars.
Next, find future value FV2 of this amount, $112,087.42, in the another account that earned 12%
annual interest rate, compounded monthly
FV2 = = 112,087.42 dollars.
Next, find future value FV2 of this amount, $112,087.42, in the another account that earned 12%
annual interest rate, compounded monthly
FV2 = 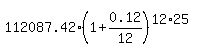 = = 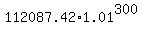 = $2,218,038.13.
ANSWER. Eugene will have $2,218,038.13 for retirement. = $2,218,038.13.
ANSWER. Eugene will have $2,218,038.13 for retirement.
Solved.
|
|
|