Question 1169683: please help me solve this equation; 
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
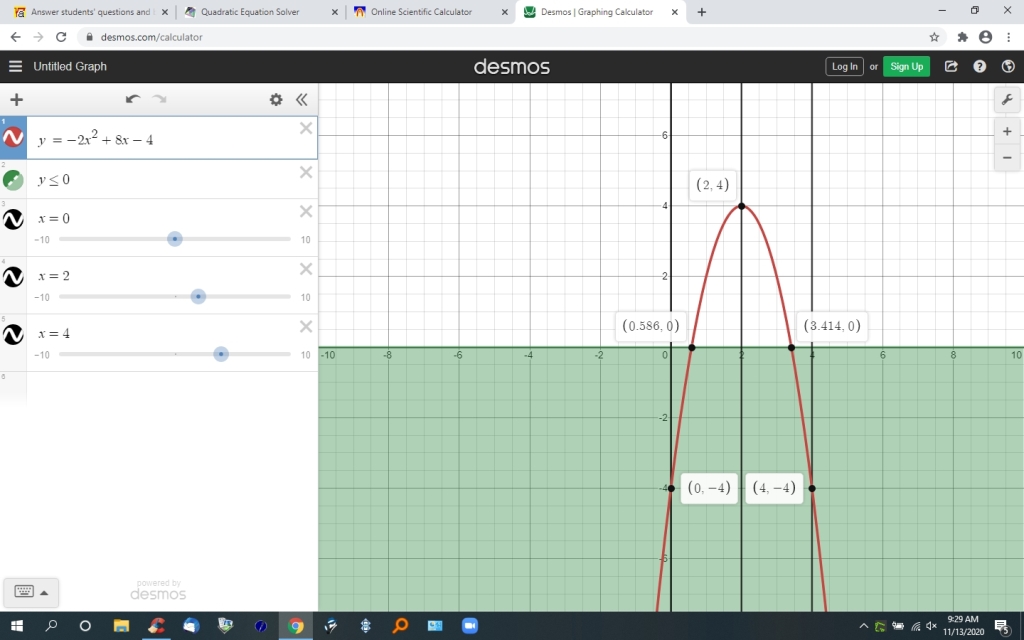
You can put this solution on YOUR website! solve for y = -2x^2 + 8x - 4
set y = 0 and switch sides to get:
-2x^2 + 8x - 4 = 0
divide both sides of the equation by 2 to get:
-x^2 + 4x - 2 = 0
multiply both sides of the equation by -1 to get:
x^2 - 4x + 2 = 0
factor the equation to get:
x = 3.4142135623731 or x = 0.5857864376269
those values of x are when -2x^2 + 8x - 4 is equal to 0.
check values in outside and in between those zero points.
i tried x = 0, x = 2, x = 4
when x = 0, the result was negative.
when x = 2 the result was positive.
when x = 4, the result was negative.
since you want to know when -2x^3 + 8x - 4 is greater than zero, that would be when .5857864376269 < x < 3.414235623731
the graph of the equation shows this to be true.
Answer by ikleyn(52925)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
please help me solve this equation; 
~~~~~~~~~~~~~~
ATTENTION (!) ATTENTION (!) ATTENTION (!)
Hello,
what is written in your post, is not an equation, at all.
It is I N E Q U A L I T Y, instead.
So, if you want to get help, then PLEASE make all necessary corrections and re-post to the forum.
If you do, then PLEASE do not post it to me personally - - - repost to the forum ONLY.
The solution for an inequality is TOTALLY DIFFERENT from that for an equation (!)
- - - End of the post - - -
|
|
|