Question 1169679: A manufacturer produces two models of racing bike, B and C, each of which must be processed through two machine shops. Machine shop 1 is available for 120 hours per month and machine shop 2 for 180 hours per month. The manufacture of each bike of type B takes 6 hours in shop 1 and 3 hours in shop 2. The corresponding times for C are 4 and 10 hours, respectively. If the profit is $180 and $220 per bike of type B and C respectively, how should the manufacturer arrange production to maximize total profit?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! objective function is profit, which you want to maximize.
the equation for that is p = 180 * x + 220 * y
x represents the number of type B bikes.
y represents the number of type C bikes.
machine shop 1 is available for 120 hours and machine shop 2 is available for 180 hours per month.
manufacture of type B bike takes 6 hours in shop 1 and 3 hours in shop 2.
manufacture of type C bike takes 4 hours in shop 1 and 10 hours in shop 2.
this means shop 1 requires 6 hours for type B bike and 4 hours for type C bike and shop 2 requires 3 hours for type B bike and 10 hours for type C bike.
this leads to two constraint equation.
they are:
6x + 4y <= 120 for shop 1
3x + 10y <= 180 hours for shop 2.
this can be seen easier in the following table.
bike type B type C capacity
type B 6 4 <= 120 hours
type C 3 10 <= 180 hours
x and y must both be greater than or equal to 0.
this leads to the following summary of requirements.
6x + 4y <= 120
3x + 10y <= 180
x >= 0
y >= 0
p = 180x + 220y is the objective function.
in the desmos.com calculator, .....
graph the opposite of the inequalities.
find the region of feasibility.
that is the unshaded region on the graph.
evaluate the objective function at each of the corner points.
the corner point with the greatest value is the solution.
the graph is shown below:
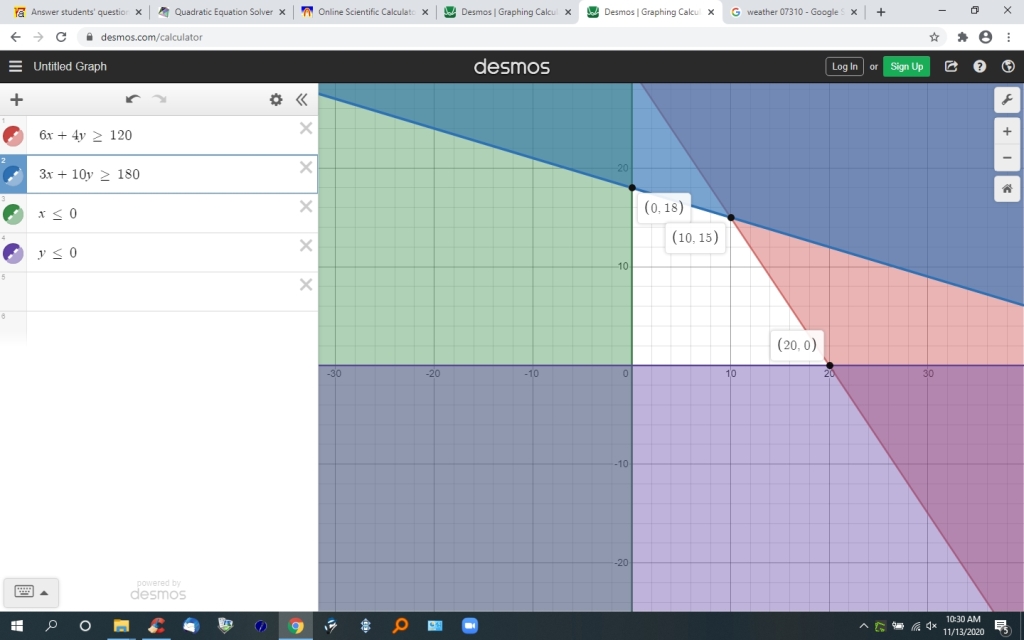
each point is in (x,y) format.
at (0,18), the profit is 0*180 + 18*220 = 3960
at (10,15), the profit is 10*180 + 15*220 = 5100
at (20,0), the profit is 20*180 + 0*220 = 3600
the maximum profit is at (10,15)
all the constraints must be met at the point (10,15)
6x + 4y <= 120 becomes 6*10 + 4*15 <= 120 which becomes 120 <= 120, so this constraint is met.
3x + 10y <= 180 becomes 3*10 + 10*15 <= 180 which becomes 180 <= 180, so this constraint is met.
x >= 0 becomes 10 >= 0, so this constraint is met.
y >= 0 becomes 15 >= 0, so this constraint is met.
all the constraints are met, so manufacture of 10 type B bikes and 15 type C bikes is the maximum profit solution.
|
|
|