|
Question 1169567: There are three options for fans purchasing a band's new release CD. They can purchase the CD, a premium CD bundle, or a deluxe CD bundle. A CD costs $7. A deluxe CD bundle costs the same as 4 CDs and one premium CD bundle. The band sells 317 CDs, 105 premium CD bundles, and 30 deluxe CD bundles for a total of $8,459. Find the price of each option.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
x = cost of a CD
y = cost of a premium CD bundle
4x+y = cost of a deluxe CD bundle
The cost of 317 CD's, 105 premium bundles, and 30 deluxe bundles is $8,459:



This is a Diophantine equation: one equation with two unknowns, with the requirement that both variables be positive integers.
Because of the size of the coefficients, it is likely that there is only one solution in positive integers.
The easiest way to find the solution(s) of an equation like this (with "large" coefficients) is with an excel spreadsheet or a graphing calculator.
Rewrite the equation as
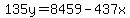

On a TI-83 calculator, enter that equation and use the table feature to find the only positive integer x value that yields a positive integer y value.
That answer is x=7 and y=40.
You can find that answer with pencil and paper, but the work is tedious.
Starting with that last equation,

simplify it by performing the division on the right to get a quotient and remainder:

Then just try x=1, x=2, x=3, and so on until you find the x value that makes the remainder 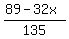 an integer. an integer.
ANSWERS:
cost of a CD: x = $7
cost of a premium CD bundle: y = $40
cost of a deluxe CD bundle: 4x+y = $68
CHECK: 317(7)+105(40)+30(68) = 2219+4200+2040 = 8459
|
|
|
| |