|
Question 116898: I am having difficulty graphing the following inequality.
3x-4y<12
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! I like to work these by converting them to the slope intercept form of:
.
y = mx + b
.
In which the equal sign actually is an inequality pointed in the correct direction.
In this slope-intercept form m (the multiplier of the x) is the slope of the line, and b,
the constant, is the value on the y-axis where the line crosses the y-axis.
.
To convert this inequality to the slope intercept form you can follow the same rules as you
would in working on an equation ... with the exception that if you multiply or divide both
sides by a negative quantity, you must reverse the direction of the inequality sign.
.
Let's do it ... you are given:
.
3x - 4y < 12
.
Get rid of the 3x on the left side by subtracting 3x from both sides. When you do that
subtraction you have:
.
-4y < -3x + 12
.
Solve for y by dividing both sides by -4. This division results in:
.
y < (-3/-4)x + (12/-4}
.
Before we proceed to simplify this, don't forget that we divided both sides by a negative
quantity (by -4) so we have to reverse the direction of the inequality arrow and we have:
.
y > (-3/-4)x + (12/-4}
.
Next do the divisions on the right side and you get:
.
y > (3/4)x - 3
.
This inequality tells you that y can have any value as long as it is greater than the
value you get when you find (3/4)x - 3.
.
But (3/4)x + 3 is the line having a slope of 3/4 and crossing the y-axis at -3. If we graph
that line it looks like:
.
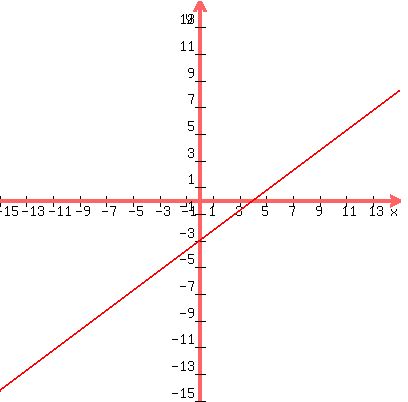
.
The inequality that we have in the slope-intercept form tells you that y must be greater than
the y value of any points that are along the graphed line. So you shade in the entire space above
the line on the graph (but not including the points on the graphed line because y must be
greater than their y value). y can have any value in the shaded area, and that translates to the
interpretation that any (x,y) point in the shaded area has as its coordinates a value of x
and a corresponding value of y that will satisfy the original inequality by making it
a true statement.
.
You can convince yourself of this by selecting any (x,y) point in the shaded area. Then
take the x and y values of that point, substitute them into the original inequality of
.
3x - 4y < 12
.
and you will see that the left side of the inequality IS LESS than the right side.
.
However, if you select an (x,y) point below the graphed line and substitute the x and y values
of that point into the original inequality, the inequality will NOT be correct. .
Similarly if you select an (x,y) point on the graphed line and substitute the x and y values
of that point into the original equality, the inequality will not be true because both
sides of it will be EQUAL ... and the left side will not be LESS THAN the right side.
.
Try it, you'll see.
.
Hope this helps you to understand this problem and how to work it. Happy New Year to you and yours.
.
|
|
|
| |