Question 1168942: a person retires 20 years from now. he wants to leave 10000 every month for 10 years after retirement the money then would be 8% compounded monthly. he has invested 50000 in a fixed deposit which pays 10% compounded quartile.how much amount at the end of every six months should he save in bank, which pays 7% compounded semi-annually.(Answers=PV of annuity=824214.81, Amount=360478.40, FV of annuity=463736.41, R=1790.011)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! here's what's happening.
in 20 years, he needs to have enough invested so that he can withdraw 10,000 every month for 10 years at 8% compounded monthly.
the present value of that annuity at 8% compounded monthly with 10,000 dollars taken out at the end of every month is equal to 824,214.81.
that amount is how much he needs at the end of 20 years.
today, he invests 50,000 at 10% per quarter for 20 years and he also invests a certain amount of money at the end of every half year for 20 years, the sum of which must be equal to 824,214.81 in 20 years.
the 50,000 invested today at 10% compounded quarterly is worth 360,478.39 in 20 years.
he needs 824,214.81.
the difference of what he needs minus what he earns on the 50,000 investment is equal to 824,214.81 minus 360,,478.39 = 463,736.42.
the amount of money he needs to invest every 6 months to equal that money at 7% per year compounded semi-annually is equal to 5484.74.
between the 50,000 he invests today and the 5484.74 that he invests every 6 months, he will have 824,214.81 invested in 20 years with which he can draw 10,000 at the end of every month for the next 10 years.
here's an online calculator that provides you with these results.
https://arachnoid.com/finance/index.html
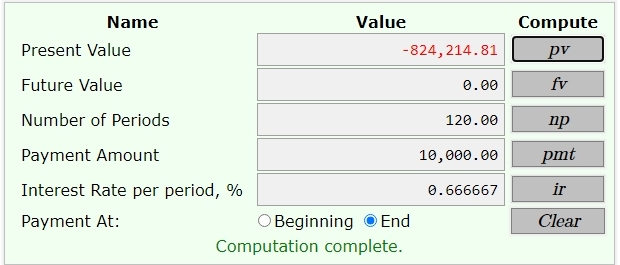
the first display is the result of finding the present value of 120 payments of 10,000 at the end of each month at 8% per year compounded monthly.
inputs were:
fv = 0
np = 10 years * 12 months per year = 120
pmt = 10,000
ir = 8% per year / 12 months per year = .6666666..... rounded to the display size.
payments made at end of each month.
output was:
pv = -824,214.81
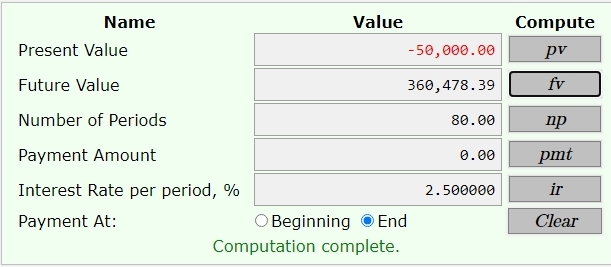
the second display is the result of finding the future value of 50,000 invested at 10% compounded quarterly for 20 years.
inputs were:
pv= -50,000
np = 20 years * 4 quarters per year = 80
pmt = 0
ir = 10% per year divided by 4 quarters pe year = 2.5
output was:
fv = 360,478.39
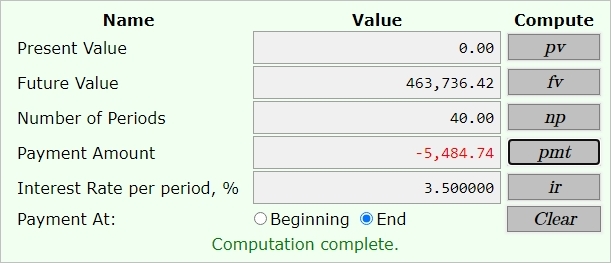
the third display is the result of finding the payments required at the end of each semi-annual period at invested 7% compounded semi-annually for 20 years that you want to be equal to 824,214.81 minus 360,478.39 = 463,736.42 in 20 years.
inputs were:
pv = 0
fv = 463,736.42
np = 20 years * 2 semi-annual periods per year = 40
ir = 7% per year / 2 semi-annual periods per year = 3.5
payments made at the end of each semi-annual period.
output was:
pmt = -5484.74
money coming in to you was shown as positive.
money going out from you was shown as negative.
|
|
|