Question 1168917: Solve the equation. (Enter your answers as a comma-separated list. Use n as an integer constant. Enter your response in radians.)
8 sec(x) csc(x) = 16 csc(x)
Found 2 solutions by MathLover1, Theo:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! your equation is:
8*sec(x) * csc(x) = 16*csc(x)
sec(x) = 1/cos(x)
csc(x) = 1/sin(x)
equation becomes:
8*1/cos(x)*1/sin(x) = 16/sin(x)
simplify to get:
8/cos(x)*1/sin(x) = 16/sin(x)
multiply both sides of the equation by sin(x) to get:
8/cos(x) = 16*sin(x)/sin(x)
simplify to get:
8/cos(x) = 16
multiply both sides of this equation by cos(x) and divide both sides of this equation by 16 to get:
8/16 = cos(x)
solve for cos(x) to get:
cos(x) = 1/2
solve for x to get:
x = arccos(1/2) = 60 degrees.
sec(x) = 1/cos(x) = 1/cos(60) = 2
csc(x) = 1/sin(x) = 1/sin(60) = 1.154700538
your equation of:
8*sec(x)*csc(x) = 16*csc(x) becomes:
8*2*1.154700538 = 16*1.154700538
simplify to get:
16*1.154700538 = 16*1.154700538
simplify further to get:
18.47520861 = 18.47520861
this confirms the solution is correct.
the solution is x = 60 degrees.
sine and cosine are both positive in the first quadrant.
sine is positive and cosine is negative in the second quadrant.
sine and cosine are both negative in the third quadrant.
sine is negative and cosine is positive in the fourth quadrant.
to test the solution, we need to look at all 4 quadrants to see if the solution is valid in any quadrant other than the first quadrant.
to confirm, we'll look at all 4 quadrants.
the equations we'll use are:
y = 16*csc(x) which we'll convert to 16/sin(x)
y = 8*sec(x)*csc(x) which we'll convert to 8/(cos(x)*sin(x))
60 degrees in the second quadrant is equal to 180 - 60 = 120 degrees.
60 degrees in the third quadrant is equal to 180 + 60 = 240 degrees.
60 degrees in the fourth quadrant is equal to 360 - 60 = 300 degrees.
we'll use the calculator to get the results.
16/sin(60) = 18.47520861.
8/(cos(60)*sin(69)) = 18.47520861
quadrant 1 is good. *****
16/sin(120) = 18.47520861
8/(cos(120)*sin(120)) = -18.47520861.
quadrant 2 is not good.
16/sin(240) = -18.47520861
8/(cos(240)*sin(240)) = 18.47520861
quadrant 3 is not good.
16/sin(300) = -18.47520861
8/(cos(300)*sin(300)) = -18.47520861
quadrant 4 is good. *****
it looks like the solution is good in the first and fourth quadrant.
in the first quadrant, they have the same value and are both positive, making them equal to each other.
in the fourth quadrant, they have the same value and are both negative, making them equal to each other.
in the second and third quadrant, they have the same value, but have opposite signs, therefore not equal.
we'll confirm further through the use of a graph, where it should be able to see when they are equal.
the graph of y = 16*csc(x) and the graph of y = 8*sec(x)*csc(x) will have the same value when they intersect.
here's the graph.
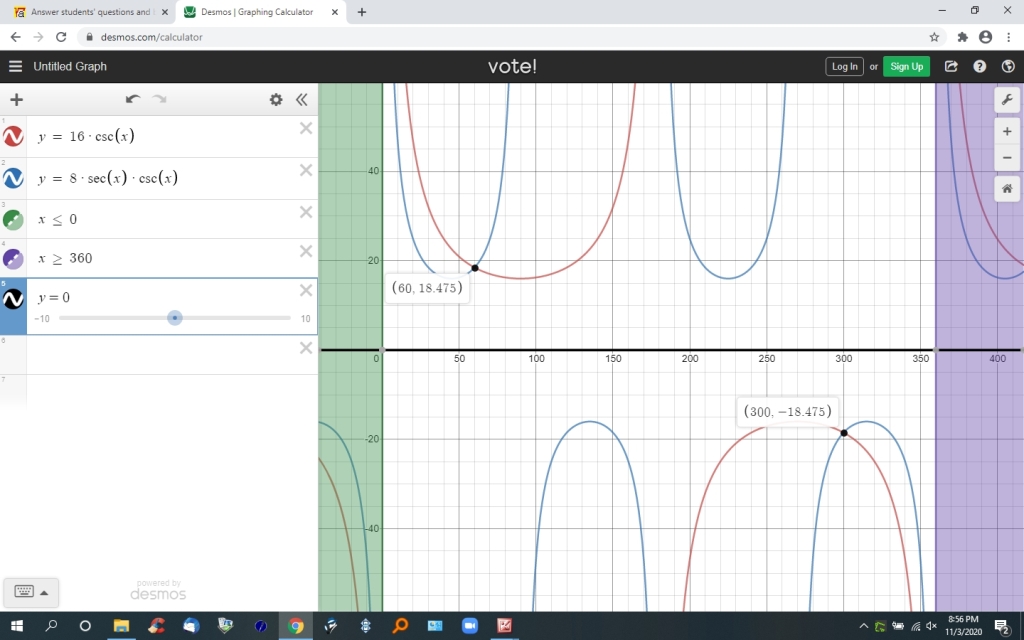
your solution in degrees is that the equation is true when x = 60 and x = 300. degrees.
radians = degrees * pi / 180.
60 degrees = 60 * pi / 180 = pi/3.
300 degrees = 300 * pi / 180 = 5pi/3.
your solution in radians is that the equation is true when x = pi/3 and x = 5pi/3.
if i had thought about it a little clearer, i might have been able to figure out what quadrant the answer would be in without testing all 4 quadrants.
in the first quadrant, sine and cosine are both positive, so sine is positive and sine * cosine is positive, making the solution good in the first quadrant.
in the second quadrant, sine is positive and cosine is negative, so sine is positive and sine * cosine is negative, making the solution not good in the second quadrant.
in the third quadrant, sine is negative and cosine is negative, so sine is negative and sine * cosine is positive, making the solution not good in the third quadrant.
in the fourth quadrant, sine is negative and cosine is positive, so sine is negative and sine * cosine is negative, making the solution good in the fourth quadrant
|
|
|