SOLUTION: Seven prizes are to be given to seven different people in a group of fourteen. In how many ways can a first prize, a second prize, a third prize and four fourth prizes be given?

Algebra ->  Probability-and-statistics -> SOLUTION: Seven prizes are to be given to seven different people in a group of fourteen. In how many ways can a first prize, a second prize, a third prize and four fourth prizes be given?      Log On


   

Question 1168172: Seven prizes are to be given to seven different people in a group of fourteen. In how many ways can a first prize, a second prize, a third prize and four fourth prizes be given?
Answer by ikleyn(52786) About Me  (Show Source):
You can put this solution on YOUR website!
.
Seven prizes are to be given to seven different people in a group of fourteen.
In how many ways can a first prize, a second prize, a third prize and four fourth prizes be given?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 

First three prizes are unique.


First  prize may go to any of 14 participants, giving 14 options.

Second prize may go to any of 13 remaining participants, giving 13 options.

Third  prize may go to any of 12 participants, giving 12 options.


So far, we have  14*13*12 options for the first three prizes.


Next 4 prizes are not unique, and we do not distinct them.  
They will go to four different people of remaining 11 people,
but the order does not matter, since the prizes of this level are indistinguishable.


So, at this step, we have 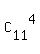 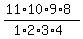C%5B11%5D%5E4 = %2811%2A10%2A9%2A8%29%2F%281%2A2%2A3%2A4%29 = 330 different options for these 4 fourth prizes.


In all, all prizes can be distributed in  14*13*12*330 = 720720  distinguishable ways.

Solved.