|
Question 116803: Find the horizontal and vertical asymptotes of the following. Type “none” if the function does not have an asymptote.
g(x)= 5x/x-1
Answer:
Horizontal:
Vertical:
Found 2 solutions by stanbon, MathLover1:
Answer by stanbon(75887)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! The horizontal asymptote tells you, roughly, where the graph will go when x is really, really big.
When the degrees of the numerator and the denominator are the same, then the horizontal asymptote is found by dividing the leading terms, so the asymptote is given by:
y = (numerator's leading coefficient) / (denominator's leading coefficient)
This is 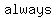 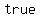 . .
 ………… this function has degree-1 polynomials top and bottom; the degrees are the same in the numerator and the denominator ………… this function has degree-1 polynomials top and bottom; the degrees are the same in the numerator and the denominator
Since the degrees are the same, the numerator and denominator "pull" evenly; this graph should not drag down to the  , nor should it shoot off to infinity. , nor should it shoot off to infinity.
Again, think in terms of  values for values for  . .
When  is really is really  , you'll have, roughly, 5 times something big divided by once something big (minus a 1) so you'll roughly have , you'll have, roughly, 5 times something big divided by once something big (minus a 1) so you'll roughly have
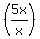 , which reduces to just , which reduces to just 
so, 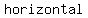  for this is for this is 
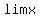 --> -->  ... ...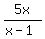 --> -->
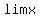 --> --> ... ... --> -->
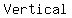 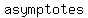 correspond to the correspond to the 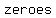 of the of the  of a rational function. of a rational function.
So, set the denominator of the above fraction equal to zero and solve, this will tell me the values that  cannot be: cannot be:

 ………..so, ………..so,  cannot be cannot be  , because then I'd be dividing by zero , because then I'd be dividing by zero
If you graph it, you will see how the graph avoid the line 
|
|
|
| |