SOLUTION: Smith is a weld inspector at a shipyard. He knows from keeping track of good and substandard welds that for the afternoon​ shift, 5% of all welds done will be substandard. If Smi

Algebra ->  Probability-and-statistics -> SOLUTION: Smith is a weld inspector at a shipyard. He knows from keeping track of good and substandard welds that for the afternoon​ shift, 5% of all welds done will be substandard. If Smi      Log On


   

Question 1168022: Smith is a weld inspector at a shipyard. He knows from keeping track of good and substandard welds that for the afternoon​ shift, 5% of all welds done will be substandard. If Smith checks 300 of the 7500 welds completed that​ shift, what is the probability that he will find less than 20 substandard​ welds? Round to four decimal places.
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235) About Me  (Show Source):
You can put this solution on YOUR website!
This is binomial with n= 300 p=0.05
can use binomcdf(300, 0.05,19) to get 0.8810 as a probability



binomial and can use a normal approximation
mean is np=300*0.05=15
variance us np(1-p)=15(0.85)=12.75
sd is sqrt (V)=3.57
z=(19.5-15)/3.57
4.5/3.57 with continuity correction factor
<1.26
probability is 0.8962, close to the exact value,

Answer by ikleyn(52832) About Me  (Show Source):
You can put this solution on YOUR website!
.
Smith is a weld inspector at a shipyard. He knows from keeping track of good and substandard welds
that for the afternoon shift 5% of all welds done will be substandard.
If Smith checks 300 of the 7500 welds completed that shift, what is the probability
that he will find less than 20 substandard welds?
~~~~~~~~~~~~~~~~~~~~~~


        In this problem,  the info about  " 7500 welds completed that shift "  is excessive.
        It does not add any sense to the problem, does not produce any influence on the solution
        and is not used in the solution. 


So, it is a binomial experiment with the number of trials n= 300.
The "success" is detecting a substandard weld.  
The probability of the individual success is p= 0.05.
The problem asks about the probability to have 19 or less individual successes.


Since the number of trials is great (more than 25), it is recommended to use
a normal approximation to binomial distribution.


For this normal distribution, the mean is  p*n = 0.05*300 = 15,

and the standard deviation is S = 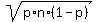sqrt%28p%2An%2A%281-p%29%29 = sqrt%280.05%2A300%2A%281-0.05%29%29 = 3.7749 (rounded).


Now you can use standard function normalcdf(z1, z2, m, S) in your regular calculator TI-83/84


    p = normalcdf(-9999, 19.5, 15, 3.7749) = 0.8834.    ANSWER


Here 19.5  is the continuity correction factor.


Alternatively, you may use an online calculator at web-site

    https://onlinestatbook.com/2/calculators/normal_dist.html

which has a convenient interface and provides a visual picture of the area of interest under the normal curve.

Solved.