Question 1167963: Many states in U.S.A have a lottery game, usually called a Pick-4, in which you pick a four-digit number such as 7359. During the lottery drawing, there are four bins, each containing balls numbered 0 through 9. One ball is drawn from each bin to form the four-digit winning number.
a. You purchase one ticket with one four-digit number. What is the probability that you will win this lottery game?
b. There are many variations of this game. The primary variation allows you to win if the four digits in your number are selected in any order as long as they are the same four digits as obtained by the lottery agency. For example, if you pick four digits making the number 1265, then you will win if 1265, 2615, 5216, 6521, and so forth, are drawn. The variations of the lottery game depend on how many unique digits are in your number. Consider the following four different versions of this game. Find the probability that you will win this lottery in each of these four situations.
i. All four digits are unique (e.g., 1234)
ii. Exactly one of the digits appears twice (e.g., 1223 or 9095)
iii. Two digits each appear twice (e.g., 2121 or 5588)
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(0) The basic version
The number of all possible outcomes is 10*10*10*10 = 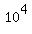 .
It means that, in all, .
It means that, in all, 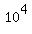 = 10000 tickets were issued.
So, the probability to win having one ticket is P = = 10000 tickets were issued.
So, the probability to win having one ticket is P = 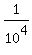 = =  = 0.0001.
version (i)
The number of all possible outcomes is 10*9*8*7 = 5040.
It means that, in all, 5040 tickets were issued.
So, the probability to win having one ticket is P = = 0.0001.
version (i)
The number of all possible outcomes is 10*9*8*7 = 5040.
It means that, in all, 5040 tickets were issued.
So, the probability to win having one ticket is P = 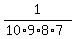 = = 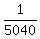 .
version (ii)
The number of all possible outcomes is .
version (ii)
The number of all possible outcomes is 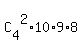 = = 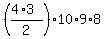 = 6*10*9*8 = 4320.
It means that, in all, 4320 tickets were issued.
So, the probability to win having one ticket is P = = 6*10*9*8 = 4320.
It means that, in all, 4320 tickets were issued.
So, the probability to win having one ticket is P = 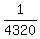 .
Version (iii)
The number of all possible outcomes is .
Version (iii)
The number of all possible outcomes is 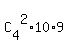 = =  = 6*10*9 = 540.
It means that, in all, 540 tickets were issued.
Thus, the probability to win having one ticket is P = = 6*10*9 = 540.
It means that, in all, 540 tickets were issued.
Thus, the probability to win having one ticket is P = 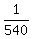 . .
Solved.
|
|
|