SOLUTION: There are values A and B such that {Bx-11}/{x^2-7x+10}={A}/{x-2}+{3}/{x-5}.Find A+B.

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: There are values A and B such that {Bx-11}/{x^2-7x+10}={A}/{x-2}+{3}/{x-5}.Find A+B.      Log On


   

Question 1167959: There are values A and B such that
{Bx-11}/{x^2-7x+10}={A}/{x-2}+{3}/{x-5}.Find A+B.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


%28Bx-11%29%2F%28x%5E2-7x%2B10%29+=+A%2F%28x-2%29%2B3%2F%28x-5%29

Multiply everything by the least common denominator, which is x%5E2-7x%2B10=%28x-2%29%28x-5%29:

Bx-11+=+A%28x-5%29%2B3%28x-2%29

Simplify....

Bx-11+=+Ax-5A%2B3x-6
Bx-11+=+%28A%2B3%29x-%285A%2B6%29

Equate the coefficients of the linear and constant terms on the two sides of the equation to give you two equations in A and B:

B+=+A%2B3
-11+=+-%285A%2B6%29

Solve the pair of equations to find the answer. I leave that easy last part to you....

Answer by ikleyn(52831) About Me  (Show Source):
You can put this solution on YOUR website!
.

I want to find the values of A and B such that this identity takes place for all x from the domain

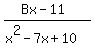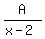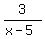    %28Bx-11%29%2F%28x%5E2-7x%2B10%29 = A%2F%28x-2%29 + 3%2F%28x-5%29.      (1)


The right side is, after writing with the common denominator

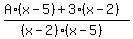    %28A%2A%28x-5%29+%2B+3%2A%28x-2%29%29%2F%28%28x-2%29%2A%28x-5%29%29.                   (2)


The denominator in (2) is the same as in the left side of (1).


Therefore, the necessary and sufficient condition for the identity to be valid is the equality
of the numerator of the left side of (1) and the numerator of (2).


So, this identuty must be held

    Bx - 11 = Ax - 5A + 3x - 6.


It implies  


    B = A + 3,          (3)

    -11 = -5A - 6       (4)


From (4),  -5A = -11 + 6 = -5;  hence  A = 1.

Then from (3),  B = 1 + 3 = 4.


So, the answer is  A + B = 1 + 4 = 5.

Solved.