|
Question 1167899: Please answer this question, I tried but I don't understand it.
Suppose a designer of a 10 ft. parabolic solar cooker wants to place the cooking pot 5 ft. above the vertex. For reference, the first considers a parabolic string with a base 10 ft. and a focus at 5 ft.from the vertex. How deep is the parabolic solar cooker?
Thank you for your help!
Answer by ikleyn(52879)   (Show Source):
You can put this solution on YOUR website! .
Please answer this question, I tried but I don't understand it.
Suppose a designer of a 10 ft. parabolic solar cooker wants to place the cooking pot 5 ft. above the vertex.
For reference, the first considers a parabolic string with a base 10 ft. and a focus at 5 ft. from the vertex.
How deep is the parabolic solar cooker?
Thank you for your help!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In this problem, you are given the size 10 ft of the opening of the parabolic solar cooker,
and the distance 5 ft from the vertex to the focus of the paraboloid (same as the place for cooking).
They want you find the depth of the parabolic mirror.
S O L U T I O N
To solve such problems, use an equation of the parabolic cross-section (which is a parabola)
in the form
y = 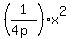 . (1)
In this form, 'p' is the focal distance, i.e. the distance of 5 ft from the vertex
to the cooking place; x is half of the opening, i.e. 10/2 = 5 ft; y is the depth of the paraboloid.
So, we substitute p = 5 ft and x = 5 ft into equation (1), and we get
y =  =  =  ft = 1 ft.
At this point, the problem is completely solved.
ANSWER. The depth of the paraboloid is 1 ft.
Solved.
|
|
|
| |
