|
Question 1167738: A function f has a horizontal asymptote of y = -4, a vertical asymptote of x = 3, and an x-intercept at (1,0). Part (a): Let f be of the form f(x) = {ax+b}/{x+c}. Find an expression for f(x). Part (b): Let f be of the form f(x) = {rx+s}/{2x+t}. Find an expression for f(x). Can you please explain in detail? Thank you!
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! For the first one, the denominator has to be (x-3) so that the vertical asymptote is x=3.
If the top is ax+b, when x gets very large or very small, the function will effectively be ax/x, since the constants won't be significant. This means a has to be -4. and now it is (-4x+b)/(x-3)
When x=1, y=0, so the numerator has to be 0 when x=1. That forces b to be 4.
f(x)=(-4x+4)/(x-3)
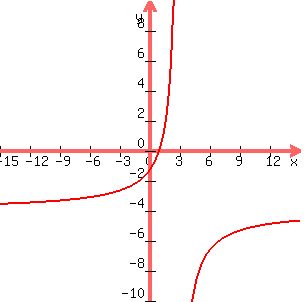
I am not clear on what is asked for in part (b). What I can say is that when rx=-s the function is 0 and that is the x-intercept.
The horizontal asymptote would be at (r/2), since when |x| gets very large the function is essentially r/2.
The vertical asymptote would be when 2x+t=0 or x=(-t/2)
|
|
|
| |