Question 1167649: Suppose u, v ∈ R3. Determine if the function
<> = 2u1v1 + u2v2 + 4u3v3
is an inner product on R3. If it is not an inner product, list the axioms which do not hold.
Found 2 solutions by ikleyn, Resolver123:
Answer by ikleyn(52884)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Suppose u, v ∈ R3. Determine if the function
⟨u, v⟩ = 2u1v1 + u2v2 + 4u3v3
is an inner product on R3. If it is not an inner product, list the axioms which do not hold.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In  , consider linear transformation
A
( , consider linear transformation
A
(  , ,  , , 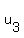 ) ----> Au = ( ) ----> Au = ( 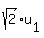 , ,  , ,  ).
It is clear that ).
It is clear that
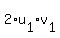 + +  + + 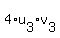 = (Au,Av).
So, the given function is an inner product.
QED. = (Au,Av).
So, the given function is an inner product.
QED.
Solved.
Answer by Resolver123(6)   (Show Source): (Show Source):
You can put this solution on YOUR website! We are given a function defined on  as: as:
(u, v) = 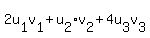
We want to determine whether this function defines an inner product on  . Recall the inner product axioms. . Recall the inner product axioms.
A function (.,.) :  -> ->  is an inner product if it satisfies the following axioms for all u, v, w in is an inner product if it satisfies the following axioms for all u, v, w in  and all scalars and all scalars  in in  . .
1. Symmetry: (u, v) = (v, u)
2. Linearity in the first argument (a.k.a. "bilinearity" for real vector spaces): (c*u + w, v) = c*(u, v) + (w, v)
3. Positive-definiteness: (u, u) ≥ 0 and (u,u)=0 if and only if u = 0.
1.) Check Symmetry
Compute both sides:
(u, v) = 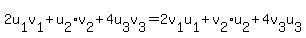 = (v,u). = (v,u).
Therefore, symmetry holds.
2.) Check Linearity in First Argument
Let u, w, v be in  and c be in and c be in  . Let’s compute: . Let’s compute:
(c*u + w, v ) = 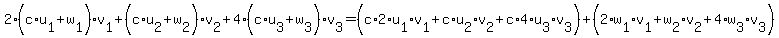 = c*(u,v) + (w,v). = c*(u,v) + (w,v).
Therefore, linearity in the first argument holds.
3.) Check for Positive-Definiteness
It must be shown that:
(u, u) = 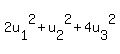 ≥ 0 and = 0 iff u = 0. ≥ 0 and = 0 iff u = 0.
Note that each term is squared and multiplied by a positive scalar, so the whole expression is non-negative.
ALso, if we let (u,u) =  , then this statement is true if and only if , then this statement is true if and only if  , i.e., u = (0,0,0). , i.e., u = (0,0,0).
Therefore, positive-definiteness holds.
Since all three axioms (symmetry, linearity, positive-definiteness) are satisfied, (u,v) = 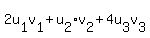 is an inner product on is an inner product on  . .
|
|
|