|
Question 1167543: A gardener has 200m of fencing to enclose two adjacent rectangular plots.what dimensions will produce a maximum enclosed area?
Answer by ikleyn(52754)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A gardener has 200m of fencing to enclose two adjacent rectangular plots.what dimensions will produce a maximum enclosed area?
~~~~~~~~~~~~~
The Figure on the right shows the condition.
In the Figure, L is the length and W is the width.
So, we have 3 pieces of fencing of the length L each and 4 pieces
of fencing of the length W each.
Then we have this equation
3L + 4W = 200,
from which we have W =  . .
|
 Figure.
Figure.
|
Next, the combined area of the two corals is
A = L*2W =  = =  = =  ,
and we have to find the length L in a way to maximize the area A, i.e. maximize the quadratic function
A = ,
and we have to find the length L in a way to maximize the area A, i.e. maximize the quadratic function
A =  . .
Now let me remind you that, if you have a quadratic function f(x) =  of the general form,
then it reaches the maximum/minimum at x = of the general form,
then it reaches the maximum/minimum at x = 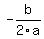 . . |
See the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
in this site.
For our situation, a =  and b = 100.
Therefore, the maximum is at L = - and b = 100.
Therefore, the maximum is at L = - 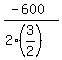 = =  = 33 = 33  .
Thus the area get a maximum at L = 33 .
Thus the area get a maximum at L = 33  feet.
Then W = feet.
Then W =  = =  = 25 feet.
Answer. The area is maximal at L = 33 = 25 feet.
Answer. The area is maximal at L = 33  feet and 2W = 2*25 feet = 50 feet. feet and 2W = 2*25 feet = 50 feet.
Solved.
-------------
See the lesson
- A rancher planning to fence two adjacent rectangular corrals to enclose the maximal area
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this textbook under the topic "Finding minimum/maximum of quadratic functions".
Save the link to this online textbook together with its description
Free of charge online textbook in ALGEBRA-I
https://www.algebra.com/algebra/homework/quadratic/lessons/ALGEBRA-I-YOUR-ONLINE-TEXTBOOK.lesson
to your archive and use it when it is needed.
|
|
|
| |