SOLUTION: Help is super appreciated! At noon, ship A is 130 km west of ship B. Ship A is sailing east at 30 km/h and ship B is sailing north at 25 km/h. How fast is the distance between t

In a coordinate plane (x.y), ship A and ship B are in the coordinate line "west - east" initially.

In standard notations, this coordinate line is horizontal  y = 0.


For ship A, its initial coordinate is (-130,0).

For ship B, its initial coordinate is (0,0).



In 4 hours, at 4:00 pm, ship A is at the point (-10,0),
                  while ship B is at the point (0,100).


The distance between the ships at t= 4:pm is

    D0 =  =  = .



The parametric form of the path for ship A is (-10 + 30t, 0);
                                for ship B    (0, 100 + 25t),
where 't' is the time after 4:00 pm.


The square of the distance between the ships in parametric form is

    D^2(t) = (-10+30t)^2 + (100+25t)^2.


Take the time derivative of both sides, considering D^2(t) as a composite function

     = 2*(-10)*30 + 2*100*25.


Simplify

     = 4400


and find the rate of the distance change between the ships

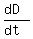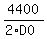     =  =  = 21.891 km/h  (rounded).    <<<---=== ANSWER