|
Question 1167264: Larry mitchel invested part of his $13,000 advance at 7% annual simple interest and the rest at 3% annual simple interest. If his total yearly interest from both accounts was $870, find the amount invested at each rate
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52775)   (Show Source):
You can put this solution on YOUR website! .
Let x = invested at 7%
Then the amount invested at 3% is (13000-x) dollars.
The total interest equation is
0.07x + 0.03*(13000-x) = 870 dollars.
From the equation
x = 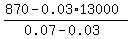 = 12000.
ANSWER. $12000 invested at 7% and the rest $1000 invested at 3%.
CHECK. 0.07*12000 + 0.03*1000 = 870 dollars of total interest. ! Correct !
Solved.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
Here is a non-algebraic method for solving a "mixture" problem like this.
(1) Find the amounts of interest if the whole $13,000 had been invested at each rate.
$13,000 at 7% would yield $910 interest; $13,000 at 3% would yield $390 interest.
(2) Where the actual interest lies between those two amounts exactly determines how much was invested at each rate.
From 390 to 910 on a number line is a difference of 520; from 390 to 870 is a difference of 480. 480/520 = 48/52 = 12/13.
$870 is 12/13 of the way from $390 to $910; that means 12/13 of the total was invested at the higher rate.
ANSWERS: 12/13 of $13,000, or $12,000, was invested at 7%; the other $1000 was invested at 3%.
CHECK: .07(12000)+.03(1000) = 840+30 = 870
|
|
|
| |
