Question 116714: hi please help me with this. this is only what i am not done with an have to hand this in tomorrow. it is already 10 at night here. I am really worried
please help me
Kayla has 1.5 m (squared) of sheet metal to build a storage box for firewood.
a) what is the surface area of the metal , in square centimeters?
b) What are the dimensions for this square based prism box with maximum volume including a lid ?
c)If the box doesnt have a lid, what are the dimensions of the square based prism. Round off to the nearest tenth of a centimeters.hint( make a table of possible boxes)
any help will be apreciated
for a) i think the area is 150 cm squared
for B according to my calculations the dimensions are 5 x 5 x 5 cm and the volume is 125 cm (cubed)
I dont know if my answers are correct and I am stuck on c)
any help will be greatly appreciated . Please help me
I need help desperately
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Desperate times call for desperate action. Here's some help. You may need to re-post this
problem to see if another tutor can supply some more info.
.
First part. The way I interpret what you wrote is that Kayla has 1.5 square meters of material.
[Note that this is NOT the same as a 1.5 meter square which is 1.5 meters on a side for
an area of 1.5^2 = 2.25 square meters.]
.
There are 10,000 square centimeters in each square meter ... think that 1 square meter could
be a metal sheet 1 meter on a side. But 1 meter is 100 cm. So a sheet of metal that is
1 meter on a side is equal to a sheet of metal that is 100 cm on a side. So a 1 meter by 1 meter
sheet of metal is equivalent to a 100 cm by 100 cm piece of material. A 100 by 100 cm sheet
is 10,000 square cm. So the conversion from square meters to square cm is 10,000 times sq meters
equals sq cm.
.
And since Kayla has 1.5 square meters of metal, 10,000 times that means that the metal Kayla
has is 15,000 square centimeters of metal.
.
Second part. I have just about convinced myself that a cube is the type of box that will
contain the maximum volume. And a cube has 6 sides (Top, Bottom, 4 Sides around). Since
a cube has equal length sides on all edges, the area of each side is S^2 and there are,
as stated, 6 sides. So the total area of material needed to make a cube is 6S^2 and this
area must come from 15,000 sq cm of metal. Solve for S by using the equation
.
6S^2 = 15000
.
Divide both sides by 6 and you have:
.
S^2 = 2500
.
Take the square root of both sides and you have:
.
S = sqrt(2500) = 50 cm
.
The box with the maximum volume that can be built from 1.5 square meters of material and
having a lid is (I think) a cube having each side 50 cm long. Not a very big box for firewood.
(That's a cube that is only about 19.6 inches by 19.6 inches by 19.6 inches.)
.
Part c.
.
If Kayla is going to build a box with no lid and a square bottom, the amount of material needed
for the bottom of the box will be 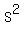 where S is a side of the bottom of the box. The where S is a side of the bottom of the box. The
question is, how tall can the box be? The material left after making the bottom of the box
is 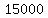 sq cm minus sq cm minus 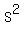 cm. Each of the four sides that need to be build will be H, the height cm. Each of the four sides that need to be build will be H, the height
of the box, times S in area. And since there are four sides, the total area of material needed
for the sides is  . Since the amount of metal left after making the bottom of the box . Since the amount of metal left after making the bottom of the box
is 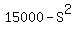 , this is the amount of material left to build the sides which requires a total , this is the amount of material left to build the sides which requires a total
of  . Set these two amounts equal and solve for H: . Set these two amounts equal and solve for H:
.

.
Divide both sides by 4*S and you have:
.

.
And we know the volume of this box is the product of its dimensions or:
.
 or or 
.
Substitute (15000 - S^2)/(4*S) for H in the volume equation to get:
.

.
Cancel one of S in the numerator with the S in the denominator and the equation becomes:
.

.
Now build yourself a table by assuming values for S and calculating the corresponding
values for the Volume.
.
If I haven't made a mistake, here's a table of some values:
.
When S (the dimension of the square bottom) = ......... then Volume =
.
60 cm ................................................. 171,000 cm^3
65 cm ................................................. 175,094 cm^3
69 cm ................................................. 176,623 cm^3
70 cm ................................................. 176,150 cm^3
71 cm ................................................. 176,772 cm^3
72 cm ................................................. 176,688 cm^3
75 cm ................................................. 175,781 cm^3
.
It looks as if the volume maximizes around the value S = 71 cm
.
And when S = 71 cm the height is given by:
.

.
So the dimensions of the box that appear to maximize the volume are around
.
71 cm by 71 cm by 35.0669 cm where the 71 by 71 is the bottom and the 35 is the height.
.
I've done this so fast I haven't had time to check it, but maybe it will help you to understand
the problem a little better and get some credit tomorrow. Check my work.
.
Hope I'm not too late.
|
|
|