Question 1167017: Rhea is 3 years younger than her friend Lisa. In seven years the product of theirs ages will be 5 more than thrice the product of their ages five years ago. The present age of Lisa is.......
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! this is quite messy because the calculations don't come out nice an clean.
i did, however, come up with a solution that appears to be good.
i don't know if the problem was intended to be so difficult to solve because most problems of this type usually give you a nice clean answer.
this one was definitely not one of those.
this is how i solved it.
let R = rhea's age now.
let L = lisa's age now.
in 7 years the product of their ages will be 5 more than 3 times the product of their ages 5 years ago.
the equation i came up for that is:
(R + 7) * (L + 7) = 3 * (R - 5) * (L - 5) + 5
breaking this down, i get:
(R + 7) * (L + 7) = RL + 7R + 7L + 49
(R - 5) * (L - 5) = RL - 5R - 5L + 25
3 * (R - 5) * (L - 5) = 3RL - 15R - 15L + 75
3 * (R - 5) * (L - 5) + 5 = 3RL - 15R - 15L + 80
your equation of (R + 7) * (L + 7) = 3 * (R - 5) * (L - 5) + 5 becomes:
RL + 7R + 7L + 49 = 3RL - 15R - 15L + 80
switch sides to get:
3RL - 15R - 15L + 80 = RL + 7R + 7L + 49
subtract the right side of the equation from both sides of the equation to get:
3RL - 15R - 15L + 80 - (RL + 7R + 7L + 49) = 0
simplify to get:
3RL - 15R - 15L + 80 - RL - 7R - 7L - 49 = 0
combine like terms to get:
2RL - 22R - 22L + 31 = 0
since R = L - 3, replace R with L - 3 to get:
2(L-3)L - 22(L-3) - 22L + 31 = 0
simplify to get:
2L^2 - 6L - 22L + 66 - 22L + 31 = 0
combine like terms to get:
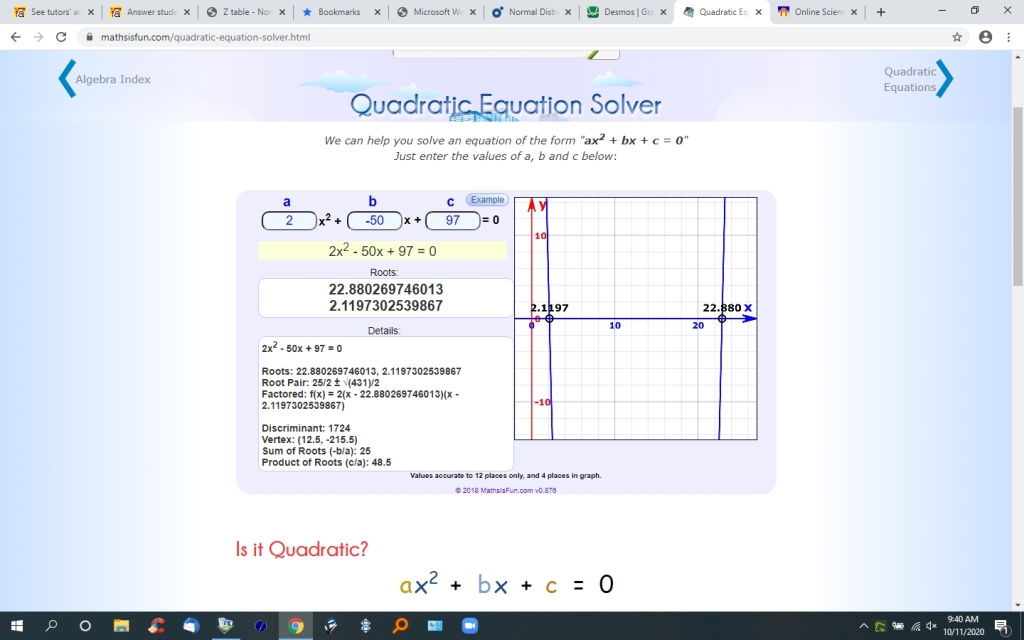
2L^2 - 50L + 97 = 0
solve this quadratic equation to get:
L = 22.880269746013 or L = 2.1197302539867
since R = L - 3, this means that:
R = 19.880269746013 or R = -0.880269746
since R can't be negative, then you get:
L = 22.880269746013
R = 19.880269746013
for your information:
i did not calculate any of this manually.
i used a calculator to solve the quadratic equation and i used another calculator to solve the problem using the values i got from the calculator that solved the quadratic equation.
the calculator i used to solve the quadratic equation can be found at:
https://www.mathsisfun.com/quadratic-equation-solver.html
the calculator i used to solve the problem using the values i got from the calculator that solved the quadratic equation can be found at:
http://www.alcula.com/calculators/scientific-calculator/#gsc.tab=0
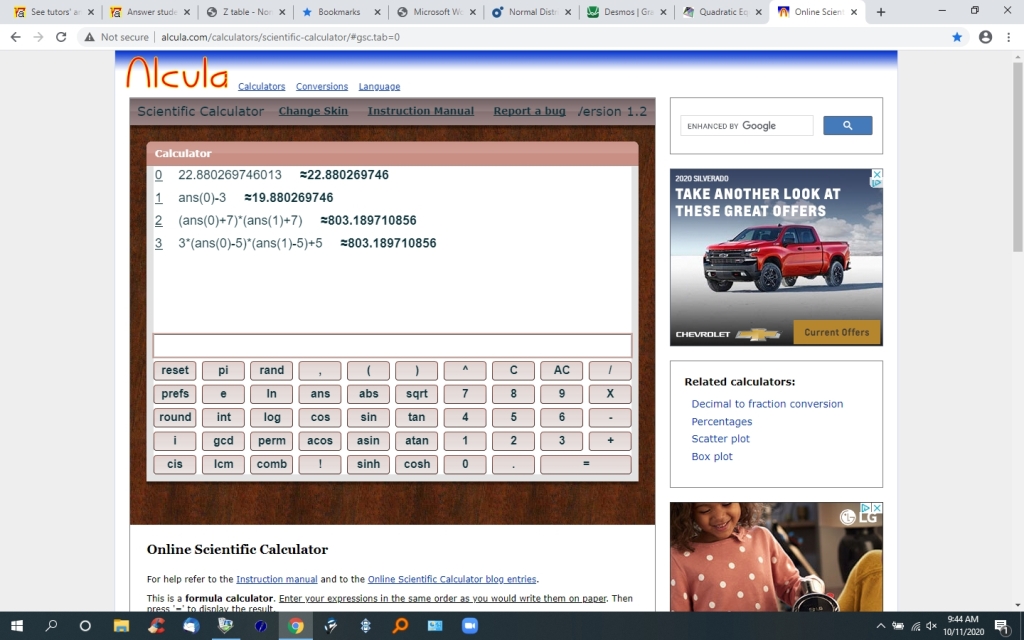
i used the values that i obtained for L and R to solve the original equations.
this was to confirm the solution was correct.
i got:
(R + 7) * (L + 7) = 803.189710856
3 * (R -5) * (L = 5) + 5 = 803.189710856
this confirms the solution is correct.
here's a display of what i got using the quadratic equation solver.
here's a display of what i got using the calculator that solved the original equations using the values i got from the quadratic equation solver.
as i said before, the calculations are quite messy.
regardless, your solution, as best i can determine, is:
Rhea is currently 19.880269746013 years old.
Lisa is currently 22.880269746013 years old.
to use the alcula scientific calculator, you need to be able to use the flash player.
Answer by ikleyn(52761)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Rhea is 3 years younger than her friend Lisa. In seven years the product of theirs ages
will be 5 more than thrice the product of their ages five years ago. The present age of Lisa is.......
~~~~~~~~~~~~~~~
This problem has no solution/solutions in whole integer numbers ----- I checked it personally . . .
If an age problem has no solution in integer numbers, it is traditionally considered as a DEFECTIVE / FAKE problem.
In other words, EITHER the problem has error in input data, OR it is recovered / retrieved
from a TRASH BIN somewhere in spaciousness Internet . . .
It is just not for the first time I see this problem posted to the forum.
I ask you, the visitor, DO NOT POST / (do not re-post) this FAKE problem to the forum.
From my side, I promise that I will delete it every time as I see it . . .
And I ask all other tutors do the same ---- thank you for understanding and your cooperation.
Hope that with joint efforts we would be able to remove this mud from the forum and from the Internet.
And finally, I ask the visitor to post your THANKS to me for opening your eyes . . .
|
|
|