SOLUTION: find the Range of f(x) = (5/(x + 1)) cos (x) , x ≥ 0

I will show here two ways to find the range.


First way is to use plotting tool like DESMOS, which you can find at the site 
https://www.desmos.com/calculator/


Print there the formula of the function, and you will get the plot immediately.


Click on the plot somewhere around the first minimum of the function in the domain x >= 0.


The plotting tool will show you the coordinates of the minimum.

They are (x,y) = (2.88997,-1.24488).


So, the minimum value of the function in the domain x >= 0 is -1.24488 (approximately).


Thus the range is [ ,  ).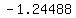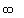


I saved the plot under this link

https://www.desmos.com/calculator/9x4t38gmur

for documentation purposes, so you can see it at any time.

To see the coordinates of the minimum of the function, click on the plot in vicinity of the minimum.



Another way to find the range is to find the minimum of the function in the domain x >= 0 using Calculus.


Take the derivative of the function and equate it to zero.


You will get an equation  tan(x) = .


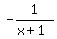It can not be solved analytically, but can be solved numerically.


Use an online calculator for solving transcendent equations

https://www.wolframalpha.com



Print there this equation tan(x) = .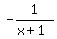


The calculator will get you a series of the roots.

Your root is the first positive number in this series x = 2.88997 (approximately).


To get the minimum of the function 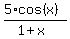,  substitute x = 2.88997 into the function.


You will get the value -1.24488 for this minimum.


So, the range of the function is  [ ,  ),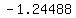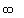


       which is the same as we found it in the first solution.