Question 1166823: A truck heads north at a constant speed of 22m/s. A car leaves 20 minutes later heading north along the same road and travelling at a constant speed of 28 m/s. Determine how long the car travels until it catches up to the truck.
20 mins = 1200 seconds, both vehicles will have the same d
I've found a solution on how to find the time, but I'm struggling to solve for t 
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website! Only two hints:
In 1200 seconds, the two vehicles are  apart.
The approach rate of the two cars is  , in  .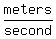
---
Handle the formula properly. Look carefully at your (single) step.
, if v is for speed, d is for distance, t is for time.
If you solve this for t, then what will you show?
Now if you have v=6 in meters per second, and d=26400 meters, then, you should understand clearly how to find the time for the catch-up.
-
 -------and if you are watching the units carefully, you see this is 4400 seconds. In HOURS this will be about 1.222 hours.
1 hour 13 minutes
|
|
|
