Question 1166818: Solve this equation. Please be sure to use the Change of Base Formula.

Found 2 solutions by ikleyn, 750033275:
Answer by ikleyn(52803)   (Show Source): (Show Source):
Answer by 750033275(2)   (Show Source): (Show Source):
You can put this solution on YOUR website! As I solved this one on my own first, I got a non-real answer of 3.2362+2.8596i. Then, I notated down: "(Unless otherwise sign change to «log (3, 35)» ➡ ≈ 3.2362 (but without the “imaginary” solution add-in))".
I am really having a very rough time trying to know what that means, but if only I could recall on an example problem in my notes, recording the exact same steps to solve the equation more properly...
As of according to my TI-84 Plus calculator, in "Real" Mode, negative logarithms are not possible as a solution, because they are not real numbers, which is probably the same thing as "√-x", which is undefined!
So, the issue here is that I have no idea what "trials" I was recently told about or why did I stop them... Perhaps, I don't think I get the whole point!...if that's what my recent tutor was trying to say.
Thus, I was rather going to put in "no solution" or "Error" as the answer as it follows: "ERR: Nonreal Answer". To be honest, I have no idea what this is all about here, trying to solve equations relative to logarithms. I'm sure I have what I needed, but it just...doesn't feel right to me!... I wonder why...
Man, Pearson-Prentice Hall has some weird references going on in their interactive worksheets, I'll tell you what... And I have never heard of what to do next in my life regarding this topic. If they were trying to pull a joke on me, I will SO not be laughing... 😠
Anyhow, I wish I could explain how to do this question more properly, but it seems to me like I haven't understood one bit of this equation, and what do I come in here for to actually deserve this kind of "undesired punishment?" ...Never mind, actually. This might be something I can't tell anyone...
So, what was I supposed to do? Trying to put in "-log (45)" as a replacement for "log (-45)"? I don't know what else to say, but this is probably not the correct answer! Face it, I'm running ALL OUT of ideas!!! 😓💭
Wait! I think I can do this... 😤 😮 😯
First, I subtract 5 from both sides of this equation, to get -40 - 5 = -45.

Then, I should check to see if both sides are in the same integer—negative!

Next, I was going to use the Change of Base Formula, but I've got a better idea!...
I should now turn -3^x=-45 into its logarithmic form.
The negative sign should be on the outside of the expression.
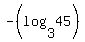
I should now have an approximate solution of 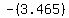 . .
This is equivalent to 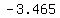 , but without the parenthesizing. , but without the parenthesizing.
Using my calculator, x will give me approximately -3.465 as my final answer.
For your information, just in case if I forgot the steps on another problem like this one, I may come back to this solution at any time, unless if my recent tutor will check if I am either right or wrong.
|
|
|