Question 1166782: I just need help with letter C and please do a step by step explanation.
A group of 8 workers decides to send a delegation of 4 to their supervisor to discuss their grievances. Complete parts (a) through (c) below.
A) How many delegations are possible?
B) If it is decided that a particular worker must be in the delegation, how many different delegations are possible?
C) If there are 3 women and 5 men in the group, how many delegations would include at least 1 woman?
Answer by ikleyn(52863)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I just need help with letter C and please do a step by step explanation.
A group of 8 workers decides to send a delegation of 4 to their supervisor to discuss their grievances.
Complete parts (a) through (c) below.
A) How many delegations are possible?
B) If it is decided that a particular worker must be in the delegation, how many different delegations are possible?
C) If there are 3 women and 5 men in the group, how many delegations would include at least 1 woman?
~~~~~~~~~~~~
In my post, I will answer parts A) and B) only.
(A) Each delegation is a subset of 4 elements of the whole set of 8 workers.
Such subsets can be chosen by different ways.
These subsets are called combinations.
If you have a set of "n" elements and select the subsets consisting of "k" elements,
then these subsets are calling "combinations of n items taken k at a time".
The number of such subsets (=such combinations) is denoted 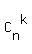 , and
there is a formula to calculate , and
there is a formula to calculate 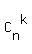 . This formula is . This formula is
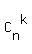 = = 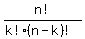 = = 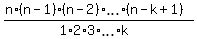 .
In particular, in your case (A), the number of possible delegations is .
In particular, in your case (A), the number of possible delegations is
 = = 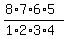 = 7*2*5 = 70.
So, the answer to part (A) is 70: 70 different delegations are possible.
Part (A) is COMPLETED.
(B) If it is decided that one particular worker must be in the delegation, then we choose only 3 remaining
members of delegation among 8-1 = 7 remaining workers.
It is = 7*2*5 = 70.
So, the answer to part (A) is 70: 70 different delegations are possible.
Part (A) is COMPLETED.
(B) If it is decided that one particular worker must be in the delegation, then we choose only 3 remaining
members of delegation among 8-1 = 7 remaining workers.
It is  different combinations, and different combinations, and  = = 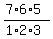 = 7*5 = 35.
It is the answer to part (B) = 7*5 = 35.
It is the answer to part (B)
------------
At this point I will stop my explanations.
Usually, students learn this knowledge from schools, from school teachers and from their textbooks.
Usually, it is not our profile at this forum to teach from scratch: as a rule, we assume that the students /(the visitors)
come to the forum just having some basic knowledge.
But in any case, from this my post you may learn these basics.
This subject, called "COMBINATIONS", can not be learned momentarily, at one instance.
It requires gradual submersion.
In this site, there are lessons devoted to this subject, so you have a unique and happy opportunity to learn from these lessons.
These introductory lessons are
- Introduction to Combinations
- PROOF of the formula on the number of Combinations
- Problems on Combinations
- OVERVIEW of lessons on Permutations and Combinations
You even may find typical solved problems there, similar to your problem.
After reading and first submersion to the subject, you may come again to the forum with the next portion of your problems and questions.
Happy learning (!)
|
|
|