SOLUTION: Find the measure of each angle. JK bisects ∠LJM, m∠LJK = (-10x + 3) , and m∠KJM = ( -x + 21). Find m∠LJM.

Don't use < for angle unless you always skip a space immediately after it,
because if you don't skip a space after it, it will often, but not always,
delete what you type after that.  Type this 
 

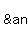for the angle symbol, and it will show up as this:

∠

Instead of doing the problem for you, I'll do one exactly like it step by
step that you can use as a model for yours.  Here is the problem I will do
for you:

Draw the picture:


   
Since CB bisects the larger angle, the two halves are equal,
so we put an equal sign between them:

-8x + 4 = -x + 25

Use the subtraction property of equality to subtract 4 from
both sides:

-8x + 4 = -x + 25
    - 4      -  4
------------------
-8x     = -x + 21

Use the addition property of equality to add +x to
both sides:

   -8x  = -x + 21
    +x    +x
------------------
   -7x  =      21

Use the division property to divide both sides by -7:

    -7x      21
    ---  =  ----   
    -7       -7  

      x  =  -3

Now since ∠ACB = (-8x + 4) we substitute -3 for x and get

         m∠ACB = -8(-3) + 4 =  24 + 4 = 28°

And since ∠BCD = (-x + 25) we substitute -3 for x and get

        m∠BCD = -(-3) + 25 = 3 + 25 = 28°

[Note: it was not necessary to do this last step because we knew they
were equal; however it is a good way to check your algebra]

So m∠ACD = m∠ACB + m∠BCD
   m∠ACD = 28° + 28°
   m∠ACD = 56°
   
Now, do your problem the same way, step by step.  

Edwin