Question 1166675: Solve and verify your answer. See Example 3. (Objective 1)
A tourist can bicycle 39 miles in the same time as he can walk 9 miles. If he can ride 10 mph faster than he can walk, how much time should he allow to walk a 35-mile trail?
9 mi39 mi
Two images are displayed.
The first image depicts a person walking with an arrow underneath them pointing to the right. This image is labeled "t hr, r mph, 9 mi."
Directly below the first image, the second image depicts a person riding a bicycle with an arrow underneath pointing to the right. This arrow extends further than the first arrow. This image is labeled "t hr, (r +10) mph, 39 mi."
First, determine how fast he can walk.
1.Let r represent the rate in mph at which the tourist can walk. Write an expression in terms of r that represents the time, in hours, it takes him to walk 9 miles.
2.Write an expression in terms of r that represents the time, in hours, it takes him to bicycle 39 miles.
3.Recall that he can bicycle 39 miles in the same time that he can walk 9 miles. Use this information to write an equation that can be used to solve for r.
4. How fast (in mph) can he walk?
How much time (in hr) should he allow to walk a 35-mile trail?
Found 2 solutions by josgarithmetic, Boreal:
Answer by josgarithmetic(39613)   (Show Source): (Show Source):
You can put this solution on YOUR website!
SPEED TIME DISTANCE
WALK r x 9
RIDE r+10 x 39
You can solve for r and then answer the question.

Once you have found r, answer the question through 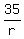 . .
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! t*r=9 miles
t*(r+10)=39 miles
t=9/r
t=39/(r+10)
cross multiply to get 39r=9r+90
30r=90
r=3 mph time to walk
will take 11 2/3 hours (35/3) to walk 35 miles.
|
|
|