Question 1166280: The height h in feet of a ball t seconds after being tossed upward is given by the function h(t) = 80t - 16t2. a. After how many seconds will it hit the ground? b. What is its maximum height? c. How long will it take to reach the maximum height?
Answer by ikleyn(52814)   (Show Source):
You can put this solution on YOUR website! .
(a) To answer this question, solve equation
h(t) = 0 = 80t - 16t^2.
The solution is t = 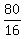 = 5 seconds.
(b) The function H(t) = -16t^2 + 80t is a quadratic function, whose plot is a parabola opened down.
This quadratic function has the maximum at the value of its argument t =  , where "a" is the coefficient at t^2
and "b" is the coefficient at t.
In your case, a= -16, b= 80, so the function gets the maximum at t = 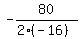 = 2.5.
So, the ball gets the maximum height 2.5 seconds after is hit straight up.
(c) To find the maximum height, calculate h(t) at t = 2.5 seconds.
 = -16*2.5^2 + 80*2.5 = 100 ft.
Solved.
----------------
On finding the maximum/minimum of a quadratic function, see the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
in this site.
On solving similar problems to yours in this post, see the lessons
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
in this site.
|
|
|
