SOLUTION: Find the intersection of two ellipse 4x^2+9y^2=36 , 9x^2+4x^2=36

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Find the intersection of two ellipse 4x^2+9y^2=36 , 9x^2+4x^2=36       Log On


   

Question 1166142: Find the intersection of two ellipse 4x^2+9y^2=36 , 9x^2+4x^2=36
Found 2 solutions by ikleyn, solver91311:
Answer by ikleyn(52786) About Me  (Show Source):
You can put this solution on YOUR website!
.

Due to symmetry, it is clear that the intersection points (x,y) have |x| = |y|.


Then from the equations


    4x^2 + 9x^2 = 36

        13x^2   = 36

          x^2 = 36/13

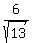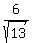      x = +/- 6%2Fsqrt%2813%29,

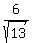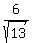      y = +/- 6%2Fsqrt%2813%29.


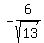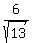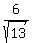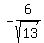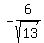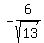ANSWER.  The intersection points are  (6%2Fsqrt%2813%29,6%2Fsqrt%2813%29),  (-6%2Fsqrt%2813%29,6%2Fsqrt%2813%29),  (6%2Fsqrt%2813%29,-6%2Fsqrt%2813%29),  (-6%2Fsqrt%2813%29,-6%2Fsqrt%2813%29).

Solved.



Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


Since both equations have the same constant term, you can set the variable terms equal to each other thus and determine the ratio between and , thus:







So the first thing we notice is that which means that the points of intersection are going to lie on the lines and , and that once we calculate one of the coordinates, we will have all of the others just by changing the signs.

Since , we can substitute into either of the equations





So the first point is



And the other three are:







Your instructor may require you to rationalize your denominators, but I leave that as an exercise for you.

John

My calculator said it, I believe it, that settles it


I > Ø