Question 1165986: its nine o'clock . how long will it be before both hands are pointing in the same direction?
Found 2 solutions by Theo, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! a full cycle of the clock is 360 degrees.
the hour hand does this in 12 hours.
therefore, the speed of the hour hand is 360 / 12 = 30 degrees per hour.
the minute hand does this in 1 hour.
therefore, the speed of the minute hand is 360 degrees per hour.
rate * time = distance.
the rate is in degrees per hour.
the time is in hours.
the distance is in degrees.
when they start, the hour hand is at 9 * 30 = 270 degrees and the minute hand is at 0 degrees.
for the hour hand, rate * time = distance becomes 30 * T + 270 = D.
for the minute hand, rate * time = distance becomes 360 * T = D.
note that 30 * T + 270 = D is equivalent to 30 * T = D - 270.
this means the hour hand needs to move 270 degrees less than the minute hand for them to be equal to the same number of degrees on the clock.
the two equations that need to be solved simultaneously are:
30 * T + 270 = D
360 * T = D
since they are both equal to D, then 30 * T + 270 = 360 * T
subtract 30 * T from both sides of this equation to get:
270 = 330 * T
solve for T to get:
T = 270 / 330 = .8181818181..... hours.
in .8181818181..... hours, .....
the hour hand will have moved from 270 degrees to 294.54545454..... degrees.
the minute hand will have moved from 0 degrees to 294.54545454..... degrees.
they will both be pointing in the same direction on the clock.
the time will be 9 + .8181818181... = 9.8181818181 hours.
that's equivalent to 9 hours and 49.0909090909... minutes.
round to the nearest minute and that becomes 9:49 on the clock.
round to the nearest second and that becomes 9:49:05 on the clock.
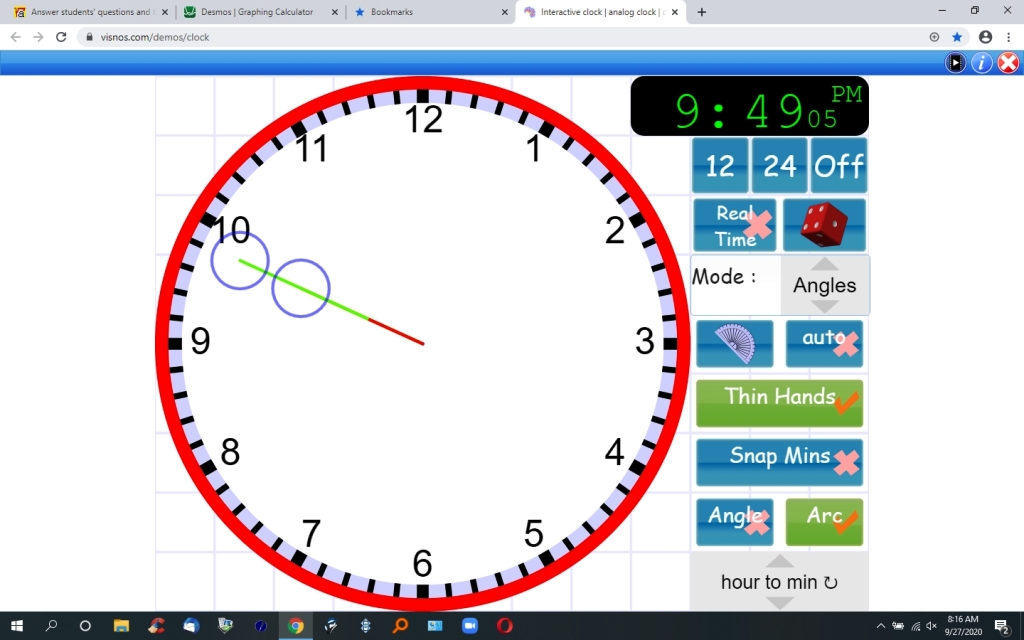
here's a visual display of what it looks like at 9:49:05 on the clock.
the hour hand is in orange.
the minute hand is in green.
you can't see the hour hand because the minute hand is covering it.
the pointer handle for the minute hand is further away from the center of the clock than the pointer handle for the hour hand.
the pointer handles are the blue circles that you see on the hands of the clock.
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In 12 hours, the hour hand makes one revolution while the minute hand makes 12. So the two hands will be pointing in the same direction 11 times in every 12 hours.
Since the rates of the two hands are constant, that means the interval between successive times that the two hands are pointing in the same direction is 12/11 hours.
The two hands are pointing in the same direction at 12:00.
The first time after 9:00 that the two hands are pointing in the same direction is 9(12/11) hours after 12:00. That is 108/11 hours, or 9 9/11 hours after 12:00, or 9/11 hours after 9:00.
ANSWER: The two hands will be pointing in the same direction 9/11 hours after 9:00.
That is 540/11 minutes, or 49 1/11 minutes, or 49 minutes 5 seconds (to the nearest second) after 9:00.
|
|
|