SOLUTION: . James has $3,000 in credit card debt, which charges 14% interest. How long will it take to pay off the card if he makes the minimum payment of $60 a month?

Use the formula which connects the loan amount with the monthly payment

    PMT = .


Here L is the loan amount, 'r' is the monthly effective interest rate, 
PMT is the monthly payments, n is the number of monthly payments (same as the number of months).


Substitute the given numbers into this equation.  You will get

    60 = .


         This equation is to find 'n'.


Simplify it step by step

     = 

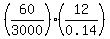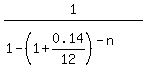    1.7142857 =     (*)

     = 1 - 1.011666667^(-n)

    0.583333333 = 1 - 1.011666667^(-n)

    1.011666667^(-n) = 1 - 0.583333333

    1.011666667^(-n) = 0.416666667

    1.011666667^n = 1/0.416666667

    1.011666667^n = 2.4

    n*log(1.011666667^n) = log(2.4)

    n =  = 75.47706349.


We must round this decimal value to the closest greater integer.


ANSWER.  It requires 76 months, or 6 years and 4 months.

As an alternative to these long calculations, we can solve equation (*) numerically,
using online solver/solvers for non-linear equations.


I did it using online calculator https://comnuan.com/cmnn03/cmnn03007/cmnn03007.php

It produced an output 75.4771, which is quite close to my answer.


You may consider it as a confirming check.