SOLUTION: hey, i need help for this :) Find the point (𝑥,𝑦) on the line 𝑦=𝑥 that is equidistant from the points (6,8) and (8,0). Can you show me the steps too please, Thank you.

Algebra ->  Linear-equations -> SOLUTION: hey, i need help for this :) Find the point (𝑥,𝑦) on the line 𝑦=𝑥 that is equidistant from the points (6,8) and (8,0). Can you show me the steps too please, Thank you.       Log On


   

Question 1165878: hey, i need help for this :) Find the point (𝑥,𝑦) on the line 𝑦=𝑥 that is equidistant from the points (6,8) and (8,0). Can you show me the steps too please, Thank you.

Found 2 solutions by josgarithmetic, KMST:
Answer by josgarithmetic(39616) About Me  (Show Source):
You can put this solution on YOUR website!
Such point on the line y=x means that vertical and horizontal coordinates are equal. Distance Formula could help.

%28x-6%29%5E2%2B%28y-8%29%5E2=%28x-8%29%5E2%2B%28y-0%29%5E2
%28x-6%29%5E2%2B%28y-8%29%5E2=%28x-8%29%5E2%2By%5E2
and x and y values on that line to be equal,
%28x-6%29%5E2%2B%28x-8%29%5E2=%28x-8%29%5E2%2Bx%5E2
%28x-6%29%5E2=x%5E2
x%5E2-12x%2B36-x%5E2=0
36-12x=0
3-x=0
highlight%28x=3%29--------------and same coordinate value as the one for y.

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
There's more that one way to do it.

CONSIDERING DISTANCES:

The square of the distance from a point (x,y) to the point (6,8) is
%28x-6%29%5E2%2B%28y-8%29%5E2
In the case the point has y=x ,
the square of that distance to (6,8) would be
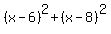%28x-6%29%5E2%2B%28x-8%29%5E2 .
The square of the distance from a point (x,y) to the point (8,0) is
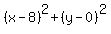%28x-8%29%5E2%2B%28y-0%29%5E2 , but if the point has y=x ,
the distance to (6,8) would be the square root of
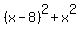%28x-8%29%5E2%2Bx%5E2 .
If the point you are looking for is at the same distance from (6.8,qnd (8,0),
those distances are the same, and their squares are the same, so
%28x-6%29%5E2%2B%28x-8%29%5E2=%28x-8%29%5E2%2Bx%5E2
%28x-6%29%5E2%2Bcross%28%28x-8%29%5E2%29=cross%28%28x-8%29%5E2%29%2Bx%5E2
%28x-6%29%5E2=%2Bx%5E2
x%5E2-12x%2B36=x%5E2
cross%28x%5E2%29-12x%2B36=cross%28x%5E2%29
-12x%2B36=0
36=12x
36%2F12=x
highlight%28x=3%29
The point we are looking for is highlight%28C%283%2C3%29%29

ANOTHER APPROACH:
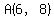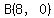
The points equidistant from A%286%2C8%29 and B%288%2C0%29
are on the bisector of segment AB.
That is the line perpendicular to AB through the midpoint of AB.
The midpoint of AB is M%28%286%2B8%29%2F2%2C%288%2B0%29%2F2%29=M%287.4%29
The slope of AB is %288-0%29%2F%286-8%29=8%2F%28-2%29=-4
The slope of a line perpendicular to AB is 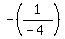-%281%2F%28-4%29%29%22=%221%2F4
The equation of the line going through M%287%2C4%29 ,
with slope M=1%2F4 is y-4=%281%2F4%29%28x-7%29 ' The intersection of that line with y=x is the point that we look for.
Besides y=x , it must comply with y-4=%281%2F4%29%28x-7%29 ,
so to find the value of x we solve x-4=%281%2F4%29%28x-7%29 .
4%28x-4%29=4%2A%281%2F4%29%28x-7%29
4x-16=x-7
4x-x=-7%2B16
3x=9
x=9%2F3 or highlight%28x=3%29
The point we are looking for is highlight%28C%283%2C3%29%29