SOLUTION: lim (x-> -inf) (x^2+4^-x)/(x^2-4^x)

To answer this question, you should apply your knowledge of Calculus.


The Calculus says that in the numerator, when  x --> ,  the term   dominates 
and goes to infinity much fster than  does.


In the denominator,  when  x --> ,  the term    dominates comparing with  .


Therefore, in whole, as x goes to  ,  the given function behaves as  .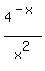


When  x --> ,  the numerator of this reduced fraction goes to infinity much faster than the denominator.


It gives the ANSWER:  the given function goes to   as  x --> .